Log In  



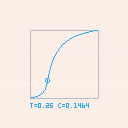
This is an implementation of the function described on this short paper:

https://arxiv.org/abs/2010.09714 (twitter thread)

It is amenable to tweeing/easing in games. I have programmed easing functions in the past and one of the problems about them is that you need to code "families of easing functions":

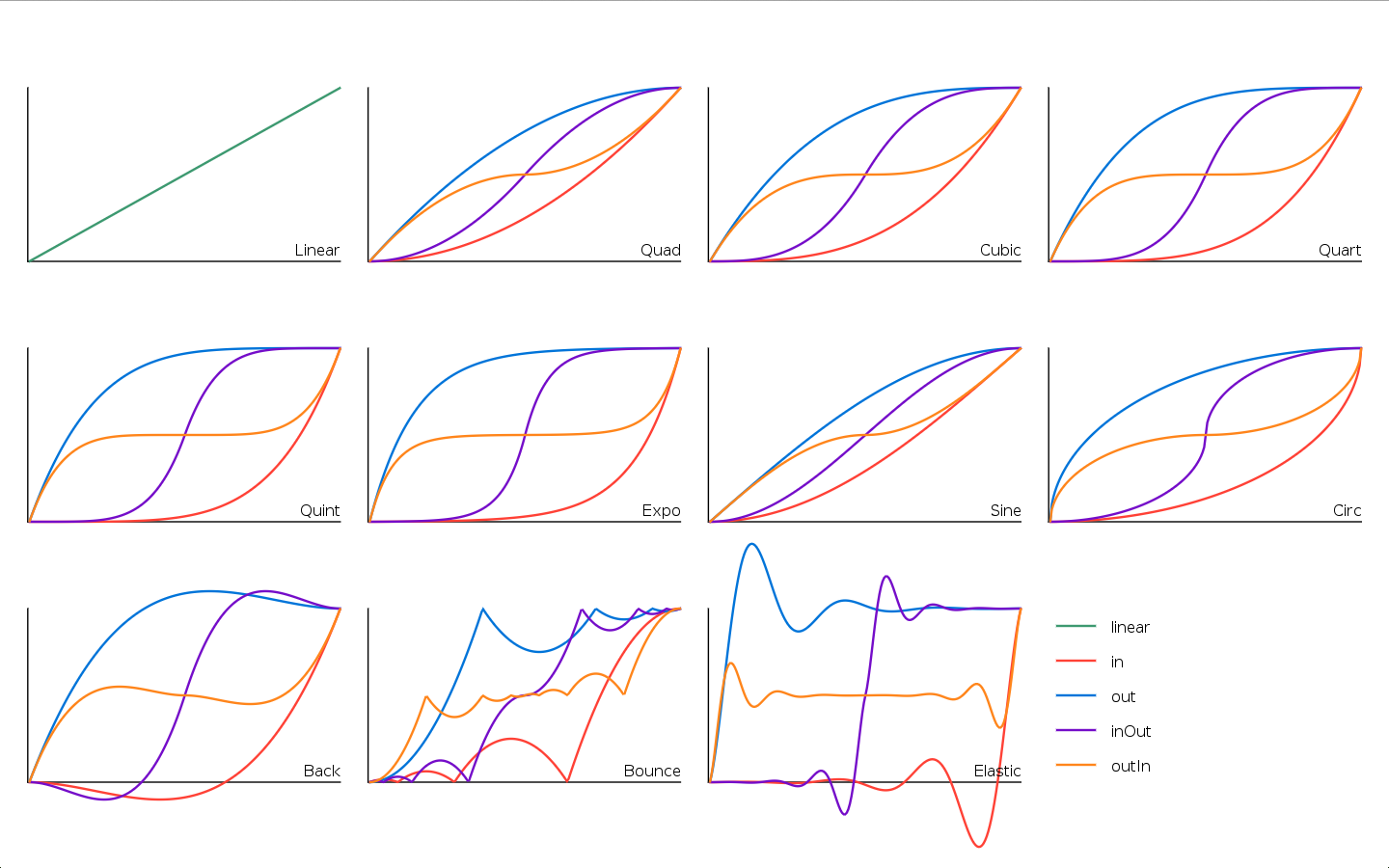
(That's from tween.lua, if you are curious).

I like this function because it can aproximate all of the "smooth families of functions" on that graph (all except the "back", "bounce" and "elastic" families) with a single function, plus it adds an infinitude of variants. Not bad for ~66 tokens.

Cart #schlick_bias_gain-0 | 2020-10-22 | Code ▽ | Embed ▽ | License: CC4-BY-NC-SA

Usage:

 
y = easing(x,t,c)

All params (x, t and c) are restricted to the [0,1] interval. When they are, the result (y) is also in the [0,1] interval.

  • x is the input being eased. In games and animations this usually encodes "the percentage of time that has passed since the start of the animation". Notice that x is restricted to [0,1]. If the magnitude you are trying to ease is not on that range, you might have to scale it (like I did in order to display the graphs).
  • t is "the threshold point" - that's the location of the "inflection" in the curve (the point at which the curve switches from out to in, or viceversa).
  • c is "the curvature". At 0-0.5 the curve will "start in in", gradually approaching linear interpolation at 0.5, and then the curve will "start in out" the more it approaches 1 from there.
  • y is the return of the easing. In games and animations this is often the "percentage of space the thing moves, for the time that has passed". Like with x, it will be on the [0,1] range, so it might need scaling.

Usually x changes over time, while t and c are "fixed" during an animation. On the attached Cartridge they are animated, but only because we show the whole curve.

There are a couple differences between my implementation and the one in the paper:

  • I had to add 1 to the x>=t branch of the function. I believe this is because Pico-8's y-axis goes "down" instead of up, like in "regular math". Not 100% sure about this.
  • The s parameter described in the paper is a "slope". When it goes from 0 to 1 it acts "one way", making the curve more "steep" at the beginning and when it goes from 1 to infinity it acts "the other way", making it more steep at the end. I replaced s with c (c = 1/(s+1)), so that it stays on the [0,1] range, like the other params.



[Please log in to post a comment]