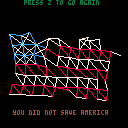
Version 2.0
Made some changes to make this thing a bit cooler:
-
Overhauled the cloth sim so it operates in 3D now. It's projected orthographically ("just uh, ignore the z value for rendering," in this case), so there's no parallax - but even so, allowing points to move on the z-axis produces much more believable motion. I'm leaving the old version up for comparison. Particularly, the mostly-intact flags don't hold themselves upright like a rectangle made of jello anymore.
-
Added basic "quad rendering." It draws two extra pixel-lines to connect pairs of simulation-lines. Makes it seem like the simulation is much higher-density than it actually is - score! (The cloth sim uses 7 rows with 10 particles each). For style, some of the simulation lines are now invisible (like the horizontal lines along unbroken stripe segments, and all the non-star diagonal structure lines)
- Added an extra prize when you win. It doesn't tell you in-game, but you can mash the "cancel" button on the victory screen to stress test it. Be careful not to hit the OK button, since that still acts as the reset button, like usual.
Version 1.0
Started messing with pico8 yesterday, and it's enough fun that I've already made three stupid doodads.
This one is, uh, sort of a game. You can win, but it's really just a clickbaity skinner box where you watch a culturally-exploitative cloth sim in various states of disrepair.
The rarest message is "GET OUT OF AMERICA." You have to mess up really bad to get it. I've literally never seen it happen, but I know that it's possible. You have to pass fewer than 40% of the line-spawn-checks (each line has a random chance to either spawn or not-spawn), but the lowest line-spawn-probability you can get for any given flag is 60%. Because of this, getting a sub-40% score is extremely rare. Maybe somebody can figure out just how rare it is.
Didn't upload the first two doodads because they weren't interactive - but here's a gif of each of them instead:
Ocean sunrise:
https://twitter.com/2DArray/status/789699736433401856
Rainy day:
https://twitter.com/2DArray/status/789940695469400064

Some amazing physics here, 2darray ! I couldn't find the code where the flag is generated as well.
Above, your rain clouds are awesome. I did something like this earlier:

Good work, Adzetko - America appreciates your compulsive somewhat-careful-button-mashing.
dw817:
Thanks! The thunder sound on your rain effect really sells it for me. (The notepad part is super cool, too!)
The flag gets generated inside _Init() - you can ctrf+f for that on the site, or it's on line 131 if you imported the cart.
Honestly it's a little messier than the rest of it, so here's a quick rundown of some important beats.
First it spawns a grid of points and stores them in a 2D table (or...a 2DArray, if you will), and then afterward it goes back through the grid and connects neighbors to each other. It also stores the same points in a 1D table, which is used for iterating once the sim starts.
makepoint() and makeline() are up at the top (lines 16 and 28), and they define our OOP-style data - a Point contains a position and an old position (no stored velocity, because we're doing Verlet integration on line 47), plus an unused starting-position. Each Line contains a reference to two point objects, and they also store an auto-detected resting-length for the connection.
Red/white/blue color choices begin at lines 170 (horizontal lines), 186 (vertical lines), and 201 ("backslash" diagonal lines). The "stars" area gets some extra crossy-lines, and the check for that begins at line 211.

Oh ... Here I am thinking that your FLAG was a series of vector points and you generated it inside a nested series of FOR/NEXT loops.
I'm watching the way the frayed pieces rotate, like on a circle. Wanted to ask you. Do you know how to make a circle or filled circle with dots only without using SIN or COS ?
I think it's possible - I just don't know how to do it.

Drawing circles without sine/cosine? Sure - a classical "good way" to do that is the Midpoint Circle Algorithm.
...But you could also do it simpler...assuming you're not worried about getting the ideal version of everything.
//radius rad=30 //center cx=64 cy=64 //do it for x=-rad,rad do // use the pythagorean theorem to find y value y=sqrt(rad*rad-x*x) pset(cx+x,cx+y,12) // mirror everything on the y axis to draw a full circle pset(cx+x,cy-y,12) end |

So this is super easy and all, but the problem with it is that it gives you some gaps at the left and right edges (because it doesn't know how to draw more than one mirrored vertical pixel per column). One option here is to increase the sampling rate near the edges, but this would take some extra math that I'm not gonna bother to figure out at the moment.
...So instead, the naive solution is to run the loop again, but do it on the other axis:
// do the above loop first, then also do this: for y=-rad,rad do x=sqrt(rad*rad-y*y) pset(cx+x,cy+y,14) pset(cx-x,cy+y,14) end |

As I said, this solution is NAIVE - it doesn't guarantee a perfect outline (might be double-thick at certain spots), and it re-draws a bunch of pixels that it's already drawn while it's cooking.

In this example, the second loop is using color #14 instead of #12, so you can tell them apart.
That fancier algorithm I linked is all about fixing the gaps perfectly without wasting any pixel-setting effort. If you want a truly ideal solution, that'll be the one. Here's the link again.
BUT...why aren't you allowed to use sine/cosine?
It's, uh, easier, and the result is arguably better:
rad=40 // draw more pixels for bigger circles // note that pixel count is literally just the circumference (pi * diameter) dotcount=3.14159*rad*2 for ang=0,1,1/dotcount do x=cx+cos(ang)*rad y=cy+sin(ang)*rad pset(x,y,12) end |

Not quite perfectly symmetrical (maybe you could fix it by subtracting .5 somewhere, or something?), but pretty dandy anyway.
Finally, just for visualization, here's what it looks like when we alternate colors for each pixel we draw in the sin/cos version (we can examine the resulting pattern to get a feel for how many of our pixels are redundant):

I dunno about the performance of sqrt vs. sin/cos in pico, but my assumption is that being less redundant with overlapping pset() calls makes this version lighter overall. Haven't measured it or anything, though, so I don't know for sure.

This is interesting stuff, 2darray ! You've got me thinking on the mechanics of it now.
How about oval, can be any size, perfectly symmetrical, no redundant drawing, filled or not, and still no SIN or COS ?
Hmm ... I like your top circle, it's "flawless" that is, no stray non-mirrored pixels nor redundancy in drawing. Lemme mess with that for a sec. Reading website you provided: https://en.wikipedia.org/wiki/Midpoint_circle_algorithm

Okay, here is the model I put together, 2darray, comparing it with PICO's own main circle routine.
function main()
cls()
color(5)
rad=30
x=63 y=63
for i=-rad,rad do
a=sqrt(rad^2-i^2)
line(x+i,y-a,x+i,y+a)
flip()
end
repeat
until btnp(4)
circ(x,y,rad,7)
verify()
end
-- verify centers w 9-dots
function verify()
for i=0,127,15.875 do
for j=0,127,15.875 do
pset(j,i,10)
end
end
end
main() -- allow at top
|
As you can see, it does not match. What code reproduces CIRC and CIRCFILL () ? I'm pretty certain it doesn't use SIN or COS as it's flawless, meaning, no rough edges or elements.

Yeah, for the pixel-perfect kinda circles, you're gonna want that algo from the wiki article.
Ovals with the first method should be easy:
// aspect ratio, like a TV aspect=1.2 // floor/ceil our outer x-values for symmetry for x=flr(-rad*aspect),-flr(-rad*aspect) do // squash x values back into a perfect-circle for y calc... y=sqrt(rad*rad-x/aspect*x/aspect) // ...but use the oval-modified x value for drawing pset(cx+x,cx+y,12) pset(cx+x,cy-y,12) end |

For more convenient oval-drawing control, you could make that function use this type of input:
drawoval(cx, cy, radiusX, radiusY)
...And then it would just use radiusY as the "actual" radius in the algorithm, and set the aspect ratio to radiusX/radiusY (or you could also do it the other way around, and use radiusX as the base radius).
If you want to rotate your oval...then you need a "rotate vector around point" function, which will involve a sin and cosine (specifically, a rotation matrix). You can just rotate the final (x,y) value before you add it to cx and cy.
aspect=1.2 rad=40 cx=64 cy=64 // rotate-a-vector and store the output in rx and ry // ang=1.0 means one-full-rotation (which is identical to no-rotation) // ang=0.125 means rotate-45-degrees rx=0 ry=0 function rotvec2(x,y,ang) sint=sin(ang) cost=cos(ang) // apply 2D rotation matrix rx=x*cost-y*sint ry=x*sint+y*cost end function _update() cls() for x=flr(-rad*aspect),-flr(-rad*aspect) do y=sqrt(rad*rad-x/aspect*x/aspect) // output of rotvec2 gets stored in rx and ry rotvec2(x,y,time()*.2) pset(cx+rx,cy+ry,12) rotvec2(x,-y,time()*.2) pset(cx+rx,cy+ry,12) end end |


Here is what I have so far.
function main()
cls()
color(5)
rad=30
x=63 y=63
for i=-rad,0,1 do
a=sqrt(rad^2-i^2)
pset(x-i,y-a)
pset(x-i,y+a)
pset(x+i,y-a)
pset(x+i,y+a)
flip()
end
repeat
until btnp(4)
circ(x,y,rad,7)
verify()
end
-- verify centers w 9-dots
function verify()
for i=0,127,15.875 do
for j=0,127,15.875 do
pset(j,i,10)
end
end
end
main() -- allow at top
|
I'm trying to figure out why it's making a bump on the bottom and not the top if it's a clone copy of pixels.
As for your code above, just think of SIN and COS as onions, and no, I don't want any. Is it possible to do the rotation you are doing minus SIN and COS ?
Or ... hmm ... lemme ask the important question. First off, with a statement. I believe you CANNOT make good circles with SIN or COS because they flop all over the place, which is why I avoid them.
x=64 y=64 rad=20 cls() for i=0,2000 do pset(x+sin(i/100)*rad,y+cos(i/100)*rad,7) end |
Here is the question now. Is it possible to make a good and flawless circle or oval maker w optional fill that is using SIN and/or COS ? Would this be easier than the earlier SQR() method ?

My assumption is that your little nubbins are coming from numeric rounding/imprecision - see if you can fix them by manually rounding stuff up or down (like the "A" value inside that first for loop, before you do the pset() calls).
Sin and cosine will give you a mathematically perfect circle - the problem is that once you map the circle onto a pixel grid by using fixed-point arithmetic, the downsampling can cause ugliness.
But - algorithms like that midpoint one are designed specifically to deal with the constraints and properties of a grid, so that still may be your best bet if you want it to be pixel-perfect.

Hmm ... you got me thinking. What if there was a way to mirror a SIN, COS ? Then it wouldn't matter how ugly, I think ...
No, still getting the NUB. So I guess the august question is, how is ZEP doing it in his code ?
How does ANY programming language provide OVAL and FILLOVAL ?

I still fully assume that pico8 is using that fancy midpoint circle algo.
The wiki article claims (at the very bottom) that the method can be generalized to work with ellipses and other shapes, but it doesn't go into any detail about what changes are necessary.

I'm reading that article you sent me in more detail. Going to see if I can dabble something interesting out of it. But yes, the ability to draw an oval (strangely missing in PICO) would help others quite a bit.
For one thing is you could have bubbles that seem to be stuck at the bottom of the screen and then suddenly wrench free giving the proper animation a bubble under those conditions, going from fat to thin and back to finally a circle again. I know I did something like this in GFA years ago.

Got it !

-- circle routine by dw817
-- (10-23-16)
-- learned from midpoint
-- circle algorithm in
-- wikipedia
-- thanks to 2darray for
-- brainstorming with me!
-- circle routine by dw817
-- (10-23-16)
-- learned from midpoint
-- circle algorithm in
-- wikipedia
-- thanks to 2darray for
-- brainstorming with me!
function main()
cls()
for i=7,50,5 do
mycircle(64,64,i)
end
repeat
until forever
end
function mycircle(x,y,r)
local i,e,s=0,0,0
while r>=s do
for i=0,7 do
pset(x+sgn(i%2*2-1)*r,y+sgn((flr(i/2)%2)*2-1)*s)
if (i==3 or i==7) r,s=s,r
end
s+=1 e+=1+2*s
if 2*(e-r)+1>0 then
r-=1 e+=1-2*r
end
end--wend
end
main() -- allow at top
|
The next challenge, maybe ? Oval.


@Connorses: Congratulations. Your country thanks you for your button-pushes.
@dw817: Fantastic work! Looks great; much cleaner than my examples. Looks waaaay fast, too. Alongside your oval variant (I think you'd need to re-do the math to update the logic inside the while loop, right?)...how about a version with a scanline fill, with the outline being optional?

Glad you like it, 2D. Yep, it's a real logic monster. :D
And yes ... that's where I get confused. If I try to draw a line from x,y to the points it's drawing to fill it in, instead it makes a mess - it's not pretty. But rather one line to plot than the 8-separate lines to plot as it was.
It's midnight, I was going to sleep on it to see if there is some way to fill a region without drawing an arbitrary line from home to each point. It's the angle of the line I think.

Seems like the trick is to only use axis-aligned lines for fills - you can find vertical pairs of pixels while you're doing that 8x mirroring loop, and your fill-lines are just connecting those pairs (one for each column that the circle occupies)

Hmm ... Apparently I rebooted my computer without saving the message I was working on.
Here it is ! I just needed to draw that line not at an angle, but true, UDLR so no dither mess.

-- circle routine by dw817
-- (10-24-16)
-- learned from midpoint
-- circle algorithm in
-- wikipedia
-- thanks to 2darray for
-- brainstorming with me!
-- usage mycircle(x,y,r,c,t)
-- x= x-coordinates
-- y= y-coordinates
-- r= circle's radius in pixels
-- c= circle's color
-- t= circle's type (1=filled)
function main()
cls()
n=1
for i=49,7,-3 do
mycircle(64,64,i,n,1)
n+=1
end
repeat
until forever
end
function mycircle(x,y,r,c,t)
local i,e,s,a,b=0,0,0,0,0
while r>=s do
for i=0,7 do
a=x+sgn(i%2*2-1)*r
b=y+sgn((flr(i/2)%2)*2-1)*s
if t==0 then
pset(a,b,c)
else
line(a,b,x,b,c)
end
if (i==3 or i==7) r,s=s,r
end
s+=1 e+=1+2*s
if 2*(e-r)+1>0 then
r-=1 e+=1-2*r
end
end--wend
end
main() -- allow at top
|
[Please log in to post a comment]