Hello.
The other day I was working in a very primitive language that did not have random numbers but could move an object - randomly.
Determined it could be done I wrote a routine that has an object start at the left of the screen.
Above that is a wall all the way across, below is blank, then another wall all the way across.
Looking a little like this:
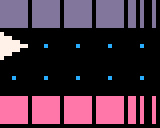
|
[40x32] |
The purple above is the top solid line, the pink below is the bottom solid line, the dots are transparent, and the triangle facing to the right is our object.
OK so for me to build a random number generator, let's say I wanted it a number from 0-31, so there would be 31-horizontal wall tiles, above and below, the arrow.
We are ready to begin:
[A]
Clear the count to zero.
[B]
Choose a random direction for the arrow to go, either up or down.
[C]
If it cannot because of a wall in the way, add one to count. If it =CAN= go in that direction, then go in that direction now without changing the index.
[D]
Every turn whether or not the arrow changed vertically, increase the arrow's horizontal position by one until you have covered all the area, in this case, 31.
[E]
If we are not at 31, go back to [B]
[F]
Add in array that display's the bell curve, the count. So it would be:
bar[count]=bar[count]+1
Now while this does give me a random number from 0-31 it also follows a nasty bell curve, as you can see here with the example going from 1 to 126 across.


And this example code I wrote to show it each step of the way:

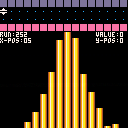
In the cart above, press or hold 🅾️ to see each step. Hold ❎ with 🅾️ to skip through it rapidly.
So my question is HOW can I make a random number generator that does not follow the bell curve and where the only thing random in the program is the ability to move an object randomly and determine collisions with it ?

To insert some mathematical jargon here, this looks like a discrete random walk with reflecting boundaries. If I'm interpreting your setup right, it seems like the bell curve you see is the distribution of the random variable X_n, where X_n is the number of times a walk of length n has bounced off the boundaries.
I'm not sure what all the constraints in your setting are, but it seems there's an easier way to get random numbers here. Instead of keeping track of how many times you bounce of the wall, you can keep track of what position it ends up at. This is a classic situation that can be modeled with Markov chains, and you can show with just a little matrix algebra and probability theory that, in the long run, the final position of the arrow is uniformly distributed. It's possible to calculate just how long "the long run" needs to be to give you the amount of randomness you want.
I don't have time right now to put together a demo (and in the two weeks since you posted this, you probably came up with a clever solution anyway), but the basic idea is to have as many positions as possible outcomes (i.e., 32 instead of 2). If physical space is a serious concern, then more problem-solving might be needed here -- maybe cleverly mixing together smaller random numbers to get a big one.
Now, having typed that all out, I realize that determining where the arrow lands may not be trivial in your language. But maybe that's at least a simpler problem to solve?

Can you increment count by more than just one? If so, you could use binary place values to generate a 5-bit binary number:
- Set
countto zero. - Randomly move the arrow up/down. If it hits a wall, add 1 to
count. - Randomly move up/down again, but this time, add 2 if it hits a wall.
- Randomly move again, conditionally adding 4 on collision.
- Randomly move again, conditionally adding 8.
- Randomly move again, conditionally adding 16.
After those six steps, count should be a number from 0 to 31. Essentially, you would be using the random up/down choice as a fair coin flip, and using that coin to generate a random binary number.
Wild hunch, asking out of curiosity: your thing doesn't happen to be related to a game called ZZT, does it?

Hi @Dbmaj7:
Actually no, I have not come up with a better solution.
Yet it was still well received in the community as a unique idea to create a random number and added to their "best of" category.
Nonetheless could you please post code to represent what it is you mean here where a true random number is chosen from 0-31 using the constraints listed ?
You can move an object one space NSEW. You cannot set any values as those are restricted. You have 10-flags that can be ON or OFF yet for this solution I would like none to be used.
You can determine if that object hits a solid object. You can randomly move EW or NS or NSEW. You can also move solid one square N S E W.
You can have more than one object on the screen at a time. Objects can call and send messages to other objects.

Hi @cmounce:
Let me see if that doesn't give me a bell-curve as well.
- 0 or 16
- 0 or 8
- 0 or 4
- 0 or 2
- 0 or 1
cls()
tab={}
for i=0,31 do
tab[i]=0
end
for i=1,1000 do
a=0
if (rnd({true,false})) a+=16
if (rnd({true,false})) a+=8
if (rnd({true,false})) a+=4
if (rnd({true,false})) a+=2
if (rnd({true,false})) a+=1
tab[a]+=1
end
for i=0,31 do
rectfill(i*4,128,i*4+3,128-(tab[i]/2)*4,7)
end
|

Looks like we have a winner !
And yes, sharp mind that you have, it is indeed old-school ZZT. Superb deduction !
[Please log in to post a comment]







