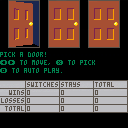
A simulation of the famous Monty Hall Problem inspired by the game show "The Price is Right."
The game goes like this:
0) 3 doors, 1 has a pile of gold coins behind it
1) You pick 1 of the 3 doors
2) Monty Hall, the show's host, opens 1 of the 2 remaining doors, revealing that it is empty
3) You are offered the chance to switch to the remaining closed door
4) All 3 doors are opened and you receive what's behind the door you ended on
The Problem:
What is the probability of winning if you switch?
What is the probability of winning if you stay?
Is it always better to switch or stay? A little of both?
Does it matter whether you switch or stay?
This cart allows you to run many trials while tracking the wins and losses to determine what the true probability is.
This is an example of a Monte Carlo simulation; experiments are repeated quickly over a long enough period to find the true probability of an event occurring. Obviously, Monte Carlo sims can give some pretty inaccurate results at first, but they get better over time based on the Law of Large Numbers.
Hope you enjoy, and thanks for playing!

Only a true gamer knows that you get the true ending by getting 100 wins without switching.
[Please log in to post a comment]