Controls
up arrow/down arrow: zoom in/zoom out
left arrow: show/hide debug information
z: multiply gravity by 10
x: turn off gravitational influence on player
Post
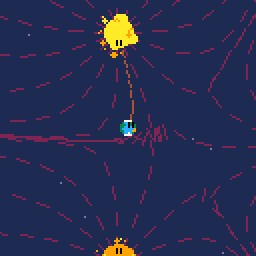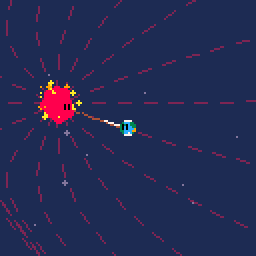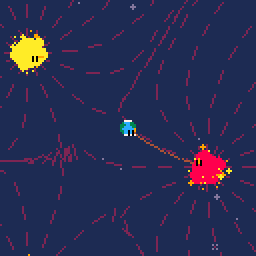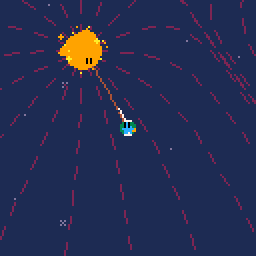
So, this is my second post. This time I'm posting some WIP of a gravity simulation I'm writing.
I'm not sure if this will ever turn into a game, maybe I'll just keep it as a "toy".
If you read "The Three Body Problem" by Cixin Liu and ever wondered how the trisolaran solar system worked, then take a look at the orbit of the planet in this simulation and imagine what it would be like, living on this planet. ;)
This cartridge implements a gravity simulation using a kind of modified newtonian gravity to make the simulation more stable for a simple toy like this.
Right now, the cart starts in "debug" mode and draws the field lines of the gravitational field as well as the current field line at the player position and the current acceleration of the player onto the screen. If you press left arrow, this debug layer is hidden.
The simulation coordinates and the drawing coordinates are decoupled via a global scaling factor. This makes it easy to implement a zoom function just by changing the scaling factor.
If you're interested in seeing different situations, you can easily add more gravitational bodies by calling 'create_body(x_position, y_position, mass, color)' in the _init function. The cart will automatically add this new body to all calculations.
The simulation
Okay, so there's a lot to talk about here, so I'll split this one up into subsections
Gravity Algorithm
I'm using the velocity Verlet algorithm to compute the gravitational acceleration that acts on the player. The advantage of using velocity Verlet is, that it is a symplectic solver. This means that energy, momentum and angular momentum are actual conserved quantities like in real life even over long simulation times. That's an advantage over the simple Euler methods as well as over more complex Runge Kutta methods, making the whole simulation much more stable.
I am however only applying this gravity to the player character, the other stellar bodies are fixed in place and are not updated using this algorithm. It would be easy to implement a full n-body simulation, but for stability and simplicity, I opted to make only the player a dynamic body.
Modified Newtonian Gravity
You might be familiar with Newtons law of gravity. If you're not then just know that according to Newton the gravitational force between two objects is proportional to the distance squared of the two bodies. So if x is the distance, then the force/acceleration will go with 1/x^2.
The "problem" for a toy model like I'm programming here is, that for small distances x<<1 this force/acceleration becomes huge. At that point you're not only running into floating point errors, you're also bound to get a very unstable system where the player planet will be slung out of the "solar system" because the force was so big. To get any kind of stable system, you would have to really carefully tweak the starting parameters of the simulation.
In real life this "problem" is solved because everything on unstable orbits got either slung into the sun or out of the solar system, so now only planets with stable orbits remain. In the simulation I really don't want anyone to wait around for billions of years to find some stable orbits.
So how do you make the simulation more stable while mostly adhering to Newtons law of gravity? The answer is simple: replace the 1/x^2 Newtonian gravity with a modified 1/(b+x^2) with a small b (if you know a bit of math: the shape of this function is the shape of a Cauchy-Lorentz distribution curve). If x is much bigger then b, then this is approximately the same as 1/x^2 but for very small x this b prevents the force from becoming too big (as the biggest possible value for the force is 1/b for x=0).
Field Lines
In analogy to field lines in electromagnetism, I decided to draw gravitational field lines to depict the gravitational force. This is trivial to do, every celestial body added to the simulation also adds 16 points along it's surface as origins for field lines. At those points the direction of the gravitational field is checked, a scaled unit vector along the same direction is drawn with a line command and at the end of said drawn line, the field is check again etc.pp.
To save on resources, this calculation is only done whenever a new celestial body is added. The field lines are static afterwards, so no need to calculate them each frame.
I also thought about representing the gravitational field via equipotential lines, but the computational expense to solve the implicit function would be much bigger, so I decided against it.

Doesn't take much to slingshot Earth right outta there. Wonder if people realize the delicate balance we have between Earth's own gravity and the Sun.

Hi dw817 thanks for commenting. :)
Yeah and as mentioned, I already took a lot of steps to make this simulation more stable than a simulation of our actual solar system.
In simulations it's quite hard to find starting configurations that lead to stable systems.
If you don't touch anything, the present system will actually be rather stable over a long period of time, but as soon as you play with the strength of the gravity all bets are off. ;)
[Please log in to post a comment]








