Hi,
I've got this grid of "slots" for enemies which I initially created using a start_x and start_y position and a couple of nested for loops to create the rows/cols with the start_x / start_y being the top left for the starting position of the grid.
But now I wanted to create the same grid but relative to an origin point at the centre - my thinking was I could increment this single point and move the grid around and maybe use sin/cos to have the slots rotate around the origin for some fun enemy patterns.
I didn't really know how to do this, so I just modified my x/y starting positions until I could get two short lines of code for the initial X/Y positions that worked. This looks fine until you move the origin point which then lags behind or in front of the actual grid.
My math is awful, so I don't really know what I'm doing wrong. I figured if the initial grid looked okay relative to the origin, I could just change the origin values and everything would fall into place at the new position in update(). But not so.
I assume it's the way I'm creating the initial X/Y positions, but I don't know how to fix it neatly.
Can somebody more math-inclined help me out?
inv_slots={}
grid_origin={x=127/2,y=40}
speed=0.25
function _init()
init_inv_slots()
end
function init_inv_slots()
local i_num=1
local width=8
local height=7
for r=1,4 do
for c=1,8 do
local i={
col=c,
row=r,
x=grid_origin.x-(c*10)+(grid_origin.x/2)+13, -- Problem here
y=grid_origin.y-(r*10)+(grid_origin.y/2)+5, -- Problem here
w=width,
h=height,
num=i_num
}
add(inv_slots,i)
i_num+=1
end
end
end
function _update60()
update_inv_slots()
end
function update_inv_slots()
if btn(0) then grid_origin.x-=speed end
if btn(1) then grid_origin.x+=speed end
if btn(2) then grid_origin.y-=speed end
if btn(3) then grid_origin.y+=speed end
--grid_origin.x+=speed
for i in all(inv_slots) do
i.x=grid_origin.x-(i.col*10)+(grid_origin.x/2)+13 -- So will be problem here too.
i.y=grid_origin.y-(i.row*10)+(grid_origin.y/2)+5 -- and here.
--if ((i.x+speed)+(i.w/2)>127 or (i.x+speed)-(i.w/2)<0) then
-- speed=-speed
--end
end
end
function _draw()
cls()
draw_inv_slots()
end
function draw_inv_slots()
for i in all(inv_slots) do
rect(i.x-(i.w/2),i.y-(i.h/2),i.x+(i.w/2),i.y+(i.h/2),7)
end
pset(grid_origin.x,grid_origin.y,8)
end |

@arashi256
Hmm I think what you want is something more like this:
local i = {
...
x=grid_origin.x-(grid_width/2)+(c*10)+13,
y=grid_origin.y-(grid_height/2)+(r*10)+5,
...
} |
In that, grid_width and grid_height are the total width and height of the grid. Subtracting half of each from the coordinate centers the grid on it, and then the offsets for the row and column are applied. This method should assign the upper-left cell first, work across horizontally to the right, then step down to the next row and repeat.
What you had before set the x-coordinate to 1.5x the origin coordinate (plus a small offset), then added columns right to left from that point. Likewise, the y-coordinate was set to 1.5x the origin (+ the offset), then rows were added bottom to top from there.
So I believe you'd wind up with something like this from what you had:
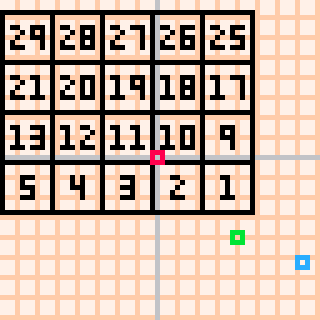
(the red coordinate is the origin, the green coordinate is the 1.5x,1.5x position, the blue coordinate is what would be the x-coordinate for c=0,r=0, and the numbers are the order they were created in, with some off-screen)

Thank you @Jusiv, I eventually got it working with:-
function init_inv_slots()
local i_num=1
local width=8
local height=7
local num_rows=4
local num_cols=8
grid_width=num_cols*width+(num_cols*2)
grid_height=num_rows*height+(num_rows*2)
for r=1,num_rows do
for c=1,num_cols do
local i={
col=c,
row=r,
x=grid_origin.x-(grid_width/2)+(c*11)-9,
y=grid_origin.y-(grid_height/2)+(r*10)-6,
w=width,
h=height,
num=i_num
}
add(inv_slots,i)
i_num+=1
end
end
end |
But now I'm trying to rotate the whole thing around the origin :D I know how to rotate in a circle at a certain radius with:-
x=origin_x+cos(angle)*radius y=origin_y+sin(angle)*radius |
So I figured the radius would actually be the distance from the origin X/Y to each slot X/Y whilst retaining the rectangular shape of the entire formation so I came up with: -
function update_inv_slots() -- assume grid_origin x/y has been updated here, although i'm actually just using -- the initial origin position. for i in all(inv_slots) do -- assuming grid_origin x/y updated, recalculate slots positions. i.x=grid_origin.x-(grid_width/2)+(i.col*11)-9 i.y=grid_origin.y-(grid_height/2)+(i.row*10)-6 -- then rotate around grid_origin i.x=grid_origin.x+cos(angle)*distance(grid_origin.x,grid_origin.y,i.x,i.y) i.y=grid_origin.y+sin(angle)*distance(grid_origin.x,grid_origin.y,i.x,i.y) end angle+=0.002 if angle>1 then angle=0 end end function distance(x1,y1,x2,y2) return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)) end |
...but this is just producing nonsense.
<sigh> I used to be able to do this. I mean, my math has never been strong but if I stray from even the simplest stuff, all my code falls to pieces.
[Please log in to post a comment]





