I stumbled upon this very odd behaviour while making this tweetcart :
https://www.lexaloffle.com/bbs/?tid=39326
After loosing some sleep over why a pixel than can randomly go in any of the 4 direction always build staircases, here is what the poor souls of the #help channel on the pico8 discord server and I have found out :
- When trying to have randomly one of these results :
dx=0 dy=1
dx=0 dy=-1
dx=1 dy=0
dx=-1 dy=0
I wrote this :
dx=rnd({-1,1}) dy=0
-- %50 chance to swap them
if(rnd({true,false})) then dy=dx dx=0 end
The behaviour disappears if I use any other method of achieving this result
- HOWEVER, the distribution of dx and dy with this method appears to really be random
- The pattern rnd({foo,bar}) appears to yield odd results, even on it's own
- if I swap out +dy and +dy2 with a -dy and -dy2 in the pset() calls, the staircase pattern is reversed.
Which makes no sense, considering the sign of dy is supposed to be 50/50
So, if anyone can explain why this behaviour happens, I'd be very grateful!

something is definitely wacky here:
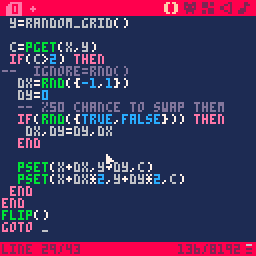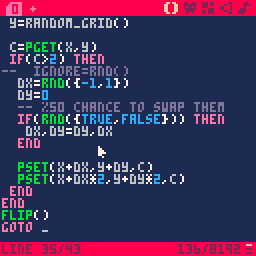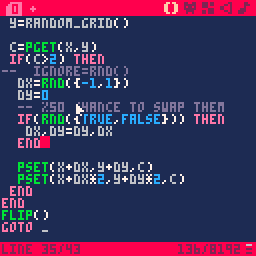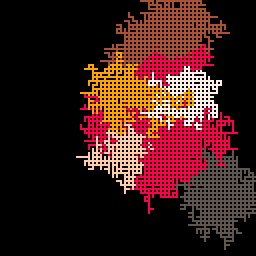
I think the issue is inside the implementation of rnd(table); if I replace it with my own custom choose() function it works fine again:

I'm still supremely stumped as to why this manifests as staircases though

I've done some playing around with it and I managed to distill the bug down to this:
x = flr(rnd(2))
y = flr(rnd(2))
z = rnd({0,1}) |
z will always equal xor(x,y).
If you pick bigger even numbers for the rnd calls and the size of the list, you will always get an odd indexed value of the list in the z call if x+y is even, and vice-versa.
Edit: I just realized this post is missing a lot more context from the discord chat I investigated it in.
This happens in your cart because you're picking a random coordinate to find a pixel to grow, then picking whether it should grow in positive or negative directions. If there's a bias where pixels with an odd x+y coordinate (before multiplying by two) always grow towards positive values and even x+y coordinates always grow towards negative values, then you get the stair shape.
Obviously there's still some investigating to do to get to the bottom of this, but I think at this point people more qualified than I am need to look into the actual rnd implementation.

okay! I think we have the full picture now: the pico-8 PRNG algorithm is pretty simple and has weaknesses/flaws; this bug is a manifestation of one of those flaws.
As valkhiya figured out, this pico-8 cart will pass the assertion all 10K times:
function test_prng_flaw(x,y,z)
return z==(x^^y)
end
cls()
print("starting")
for i=1,10000 do
x=rnd(2)\1
y=rnd(2)\1
z=rnd({0,1})
assert(test_prng_flaw(x,y,z))
end
print("prng is flawed") |
(see their explanation for why this creates staircase behavior)
Why is that property always true?? well, a friend and I looked at the decompiled code for pico8.exe; the relevant part is this:
unsigned int _p8_m_high=0x1234567;
unsigned int _p8_m_low=0xDEADBEEF;
unsigned int __cdecl pico8_random(unsigned int a1)
{
unsigned int v1; // edx
v1 = 0;
if ( a1 )
{
_p8_m_high = (_p8_m_high << 0x10 | _p8_m_high >> 0x10) + _p8_m_low;
p8_m_low += p8_m_high;
v1 = p8_m_high % a1;
}
return v1;
} |
Using this code, and some knowledge of how pico-8's fixed-point decimals works, I wrote this c program that checks for the same prng flaw as the pico-8 cart at the top of this post:
#include <stdio.h>
#include <assert.h>
// prng
// takes and returns a pico-8 number:
// the high 16 bits are the integer part;
// the low 16 bits are the fractional part
unsigned int _p8_m_high=0x1234567;
unsigned int _p8_m_low=0xDEADBEEF;
unsigned int _pico8_random(unsigned int n) {
unsigned int result = 0;
if (n != 0) {
// advance the rng state
_p8_m_high = (_p8_m_high << 0x10 | _p8_m_high >> 0x10) + _p8_m_low;
_p8_m_low = _p8_m_low + _p8_m_high;
result = _p8_m_high % n;
}
return result;
}
int test_prng_flaw(int x, int y, int z) {
return z==(x^y);
}
// returns a double between 0 and n
// simulates pico-8's rnd, except that we return a double
// (p8 returns a fixed-point value; this does not matter for this
// test, but it's worth pointing out)
double rnd(int n) {
return ((double)_pico8_random(n << 16))/(1<<16);
}
// in pico-8 rnd(table) returns a random element of table.
// this function returns the _index_ that pico-8 chooses;
// i.e. rnd(table) in pico8 can be simulated in c with
// arr[choosei(n)] (where n is the array length)
int choosei(int n) {
return _pico8_random(n);
}
int main() {
printf("starting\n");
for (int i=0; i<10000; ++i) {
int x=(int)rnd(2);
int y=(int)rnd(2);
int z=choosei(2);
assert(z==0 || z==1);
assert(test_prng_flaw(x,y,z));
}
printf("prng is flawed\n");
} |
Here are the results of running this:
$ clang test.c && ./a.exe starting prng is flawed |
I can't tell you exactly why this PRNG algorithm is flawed in this way, but this c test has satisfied me that the issue is entirely in the choice of PRNG and not some other bug lurking in pico-8.
The interesting part of all of this IMO is how this flaw manifests as staircases, as valkhiya explained above
update: okay, it turns out I can tell you exactly why this PRNG algorithm is flawed in this way :)
I'm not going to attempt to properly explain this code (clear communication is too hard), but this commented C program tries to explain exactly how the PRNG algorithm ends up producing the z==(x^^y) property:
// run this with `clang proof.c && ./a.exe`
#include <stdio.h>
#include <assert.h>
typedef unsigned int u32;
int bit(int b, u32 x) {
return (x&(1 << b))!=0;
}
u32 _p8_m_high=0x01234567;
u32 _p8_m_low =0xDEADBEEF;
u32 _pico8_random(u32 n) {
if (n == 0) return 0;
u32 swap=(_p8_m_high << 16 | _p8_m_high >> 16);
u32 old_low=_p8_m_low;
_p8_m_high = swap + old_low;
_p8_m_low = swap + (old_low<<1);
// notice:
// * (bit(3,n) means the 3rd-least-significant bit of n)
// * Property 1: bit(0,_p8_m_high) == (bit(0,swap)+bit(0,old_low))%2
// * Property 2: bit(0,_p8_m_low) == bit(0,swap)
return _p8_m_high % n;
}
void test() {
// Lowercase letters are placeholders for bits,
// different from each other and not important
// Uppercase letters are variables that always hold
// the same value throughout this calculation;
// i.e., iff A is 1 at the start, it is still 1 at the end
_pico8_random(100);
u32 x=_p8_m_high;
// _p8_m_high = 0xaaaaaaaa aaaaaaaA bbbbbbbb bbbbbbbb // new var: A
// _p8_m_low = 0xcccccccc cccccccc dddddddd dddddddd
_pico8_random(42);
// swap = 0xbbbbbbbb bbbbbbbb aaaaaaaa aaaaaaaA // notice: A
u32 y=_p8_m_high;
// _p8_m_high = 0xeeeeeeee eeeeeeeE ffffffff ffffffff // new var: E
// _p8_m_low = 0xgggggggg gggggggg hhhhhhhh hhhhhhhA // A ends up copied here (Property 2)
_pico8_random(1337);
// swap = 0xffffffff ffffffff eeeeeeee eeeeeeeE // notice: E
u32 z=_p8_m_high;
// _p8_m_high = 0xiiiiiiii iiiiiiii jjjjjjjj jjjjjjjJ // new var: J=(E+A)%2 (Property 1)
// _p8_m_low = 0xkkkkkkkk kkkkkkkk llllllll llllllll
// notice:
// * J=(E+A)%2 (follows from Property 1)
// * (E+A)%2 == E xor A
// (can be proved easily by looking at all 4 possible values for A and E)
// * proof completed!
assert(bit(0,z)==(bit(16,x)^bit(16,y)));
}
int main() {
for (int i=0; i<10000; ++i) {
test();
}
} |
(note that the PRNG algorithm has been changed because of this thread! the changed happened in v0.2.2)

Thank you so much for this investigation, I'm really happy to finally understand why it's making this pattern c:
[Please log in to post a comment]









