I'm using the code below, but it's quite a lot of tokens when converted to Lua. Does anyone have a more compact routine for use with Pico-8?
http://www.jeffreythompson.org/collision-detection/line-rect.php

see ray/aab or line/aab in: http://www.realtimerendering.com/intersections.html
but yes, math is token heavy :/

Thanks for the link. I wonder if it is beyond the remit of pico-8 to include functions like this within it? Once you have a set of various collision routines, you might already have lost 500+ tokens.

not going to happen - make sure you focus on what is really required for your game.

I wrote a line v. rect collision function for my game Sinking Ships, based on the same links provided. The token count should be fairly tight, but I needed to know which side of the rectangle I was hitting-- if you don't need that information, it could be much tighter.
Source code here: https://github.com/musurca/sinkingships/blob/master/sinkingships.p8.lua
(search for 'collision_line_rect')

Howdy! New PICO-8 user, first time poster but I can definitely help you with this one. (I've published professionally about intersection algorithms.)
Here's a compact routine you can try that weighs in at 80 tokens:
-- line/rect intersect test by aek. -- cc0 (but credit appreciated). function line_rect_isect(x0, y0, x1, y1, l, t, r, b) local tl, tr, tt, tb = (l - x0) / (x1 - x0), (r - x0) / (x1 - x0), (t - y0) / (y1 - y0), (b - y0) / (y1 - y0) return max(0, max(min(tl, tr), min(tt, tb))) < min(1, min(max(tl, tr), max(tt, tb))) end |
Note that there's a boundary condition here where the if the line merely touches the edge of the rectangle then it doesn't count as an intersection. It also does not detect intersections with zero-width or zero-height rectangles. If any of that's a problem, you can easily fix it by padding your rectangle.
On the other hand, unlike the code in the link in your post, this routine correctly detects the case where the line is completely inside the rectangle and counts that as an intersection.
Mysterious, no? So how does it work? It's built on the "slabs" method. Imagine your rectangle as the region where you have the intersection of two infinitely long slabs: one slab extending horizontally and the other extending vertically. Now imagine the line is extended out to infinity as well:
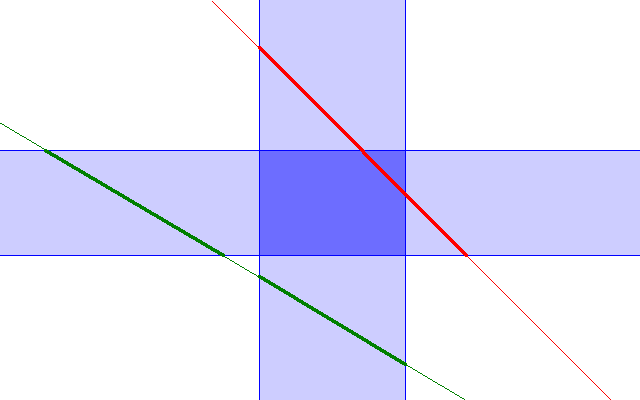
For there to be an intersection between the line and the rectangle, the 1D intervals where the infinite line intersects the two slabs must also have an intersection. In the example of the green line the two intervals are disjoint so it cannot intersect the rectangle. On the other hand, the red line does intersect the rectangle and the intersection of the two intervals exactly corresponds to where the line passes through the rectangle.
Now we don't really want to intersect an infinite line with the rectangle. We want a line segment instead. So the solution to that is simple: we make the segment between the two endpoints into a third interval, parameterized from 0 to 1, and require that all three intervals intersect.
Testing for the intersection of the intervals is pretty straightforward. We compare the maximum of the beginning points against the minimum of the end points. If the last beginning point comes before the first end point then the two give us the intersection where all three intervals overlap and we have hit. If not, then either the infinite line misses the rectangle or hits it but outside of the line segment that we care about.
You might wonder about the case where we have either a perfectly horizontal or vertical line segment, or where the two points are the same. Fortunately, the way that PICO-8 handles division by zero gives us exactly the "infinite" or degenerate intervals that we want and so we can ignore those cases and it all just works out.
Attached is a cartridge with the above code and a small test harness. Move the line and rectangle vertices with the dpad. Cycle between which to move using the buttons. The line will change between green and red depending on whether an intersection is detected.

Thanks for the suggestions everyone. I will go with aek's solution as it's the smallest. I'm near the end of developing my game and am rapidly running out of tokens.

@aek slight change to save 8 tokens at the expense of readablity.
function line_rect_isect2(x0, y0, x1, y1, l, t, r, b) local function minusx0(x) return x-x0 end local function minusy0(y) return y-y0 end local tl, tr, tt, tb = minusx0(l) / minusx0(x1), minusx0(r) / minusx0(x1), minusy0(t) / minusy0(y1), minusy0(b) / minusy0(y1) return max(0, max(min(tl, tr), min(tt, tb))) < min(1, min(max(tl, tr), max(tt, tb))) end``` |

@SquidLight actually I can't see the advantage there:
- that doesn't save but adds 8 tokens;
- the performance dramatically drops (x4 slower).
Stress-test calling 2048 times per frame:
- aek's 30/30 0.57 👌
- yours 15/30 2.15 👀
One small improvement I can think of is:
function line_rect_isect(x0, y0, x1, y1, l, t, r, b)
local xm,ym=x1-x0,y1-y0
local tl, tr, tt, tb =
(l - x0) / xm,
(r - x0) / xm,
(t - y0) / ym,
(b - y0) / ym
return max(0, max(min(tl, tr), min(tt, tb))) <
min(1, min(max(tl, tr), max(tt, tb)))
end |
- Saves 3 precious tokens;
- and gains an imperceptible 0.01 of performance in the same stress-test (30/30 0.56)

you can drop 0 in max(0,..)
and would drop min/max pairs:
if(tl>tr) tl,tr=tr,tl if(tb>tt) tb,tt=tt,tb return max(max(tl,tb))<min(1,min(tr,tt)) |
note: cannot bench it atm…

@freds72
it's adding 7 tokens 😥 but very well spent in terms of performance.
Using the same stress-test (see above) your fix makes it 1/5 faster: 0.45 👍👍

@Heracleum, I've just checked again.
original 96 tokens updated 88 tokens
one line tested against 2 boxes makes so little difference to CPU to be negligible.
Oh and checking yours I don't see three tokens saved I see it drop from 96 (original) to 77 so yours is best.

I meant in relation to the excellent aek's function, that is 80 tokens.
[Please log in to post a comment]