Just a few things I thought I’d share. Sorry if it’s gibberish and/or uninteresting to most people.
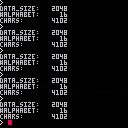
Many carts store extra data in the code section, most of the time inside strings. Some people will store structured data such as JSON or JSON-like data and let the PICO-8 compression mechanism deal with it, but you must have seen people who rolled their own compression mechanism and use custom formats such as modified base64 that takes advantage of the 59 “good” characters (i.e. the ones that needed only one byte of storage in the .p8.png format instead of two).
-- custom base64 data
local data = "e*!jfg57yfl+[7dmrin_bt#0/g6!1y68(.xh.ata_kn3j7!un_s+jn5..a)s8xi/ou0/{ff)ec}["
|
Such base64 data encodes 6 bits of information per character, and requires an average of 8.625 bits per character on the old format cartridge (pre-0.2.0). It means that this “alphabet” gave us about 5.565 bits of information per byte on the cartridge (8 * 6 / 8.625).
The new compression format is now charset-agnostic; there is no reason to use custom encodings and favour those 59 characters. We can therefore use standard base64 as far as only storage is concerned (when thinking about decoder complexity, using a contiguous alphabet would be smart):
-- base64 local data = "RpUpAUT80Jf6CQakfKLHz+1BSpUxFUYa/JDtdeAo4cyC1tHDx6gpazu0kdJqFdX+e4rMvfA+Ua0L" |
This data still encodes 6 bits of information per character, but now requires an average of 8 bits per character on the new format cartridge, giving us exactly 6 bits of information per byte on the cartridge (better than the old compression method).
So I wondered: what about other alphabets? (of more or less than 64 characters)
Here are the theoretical results, assuming perfectly random data and ignoring the fact that the compression algorithm may emit back references:
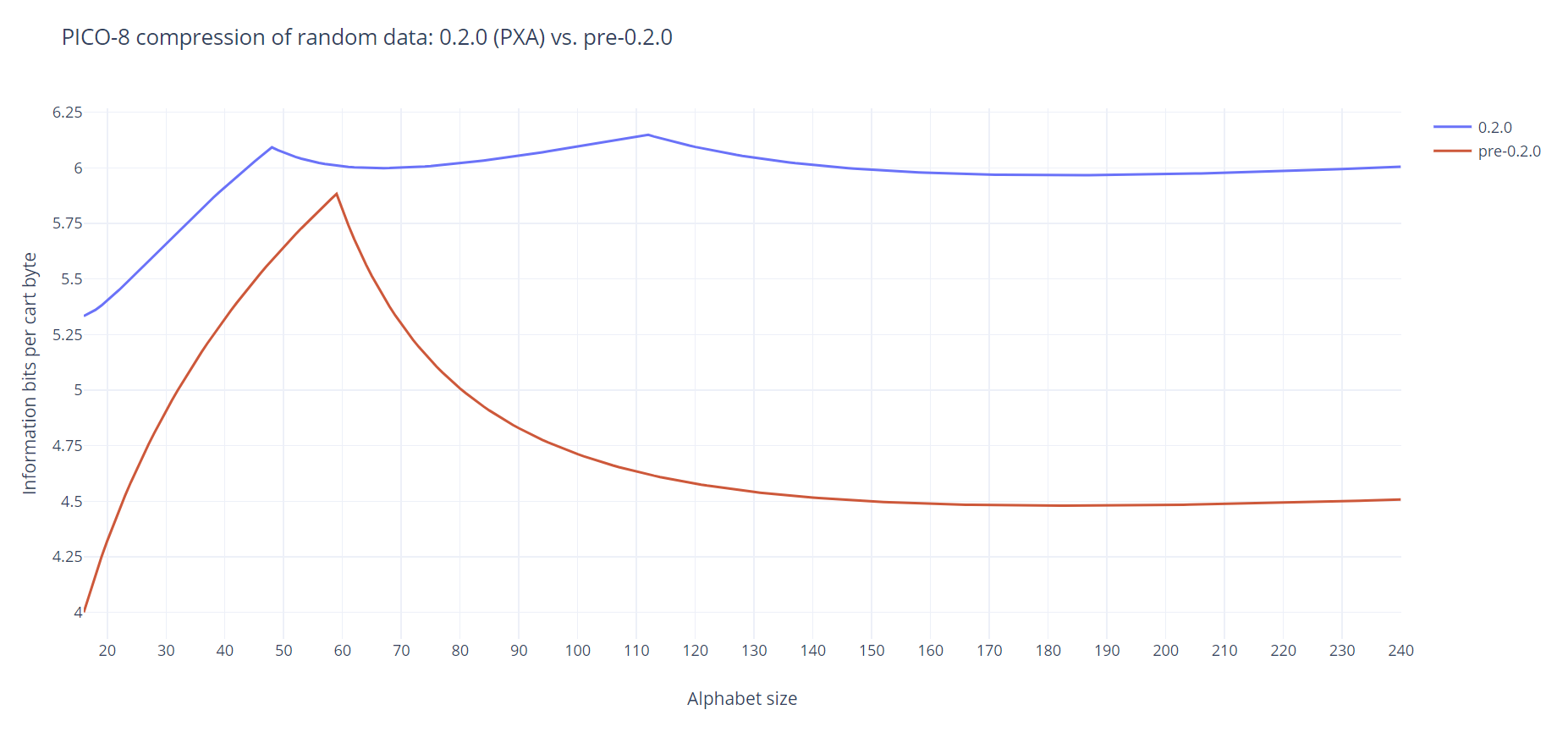
Here are my conclusions:
- the new compression algorithm always outperforms the old one for random data
- starting from about 40, alphabet size no longer really matters (there are “peaks” around 48 and 112 but probably not worth exploiting)
In a future post I will study the effect of the back reference emission (which are rare on random data but non-negligible with small alphabet sizes), but I’ll wait for 0.2.0e to be out since Zep mentioned on Twitter that he fixed something in the compression.

Note: python code for the above graph is here:
import math
for n in range(16,241):
# using an alphabet of n characters lets us encode inbits per char
inbits = math.log2(n)
# New algorithm: the 16 most recent characters need 6 bits for
# storage, the following 32 need 8, the following 64 need 10, etc.
# Assuming random data we just average these.
newbits = 6 if n < 16 else \
(6 * 16 + 8 * (n - 16)) / n if n < 48 else \
(6 * 16 + 8 * 32 + 10 * (n - 48)) / n if n < 112 else \
(6 * 16 + 8 * 32 + 10 * 64 + 12 * (n - 112)) / n if n < 240 else \
(6 * 16 + 8 * 32 + 10 * 64 + 12 * 128 + 14 * (n - 240)) / n
# Old algorithm: 59 "good" characters compress to 1 byte, all the
# others need 2 bytes.
oldbits = 8 if n < 59 else \
(8 * 59 + 16 * (n - 59)) / n
print(n, 8 * inbits / oldbits, 8 * inbits / newbits)
|

Interesting. Have you tried comparisons with hexadecimal? I recently did a simple test of max. storage capacity with hex vs base64 encoding of random data up to 100.00% cart capacity, and found only about a 2% advantage for the latter, I wonder if someone else could test that out using different methodology.

Have you checked your results again now that zep fixed a bug where some portion of the cart may not actually have been getting compressed?

Hmm, hadn't heard about that, I'll retry and post the results.

Previous test results:
avg max b64 storage: 11,845 bytes
avg max hex storage: 11,628 bytes
New test results using 0.2.0e:
avg max b64 storage: 11,872 bytes
avg max hex storage: 11,634 bytes
So no significant change.

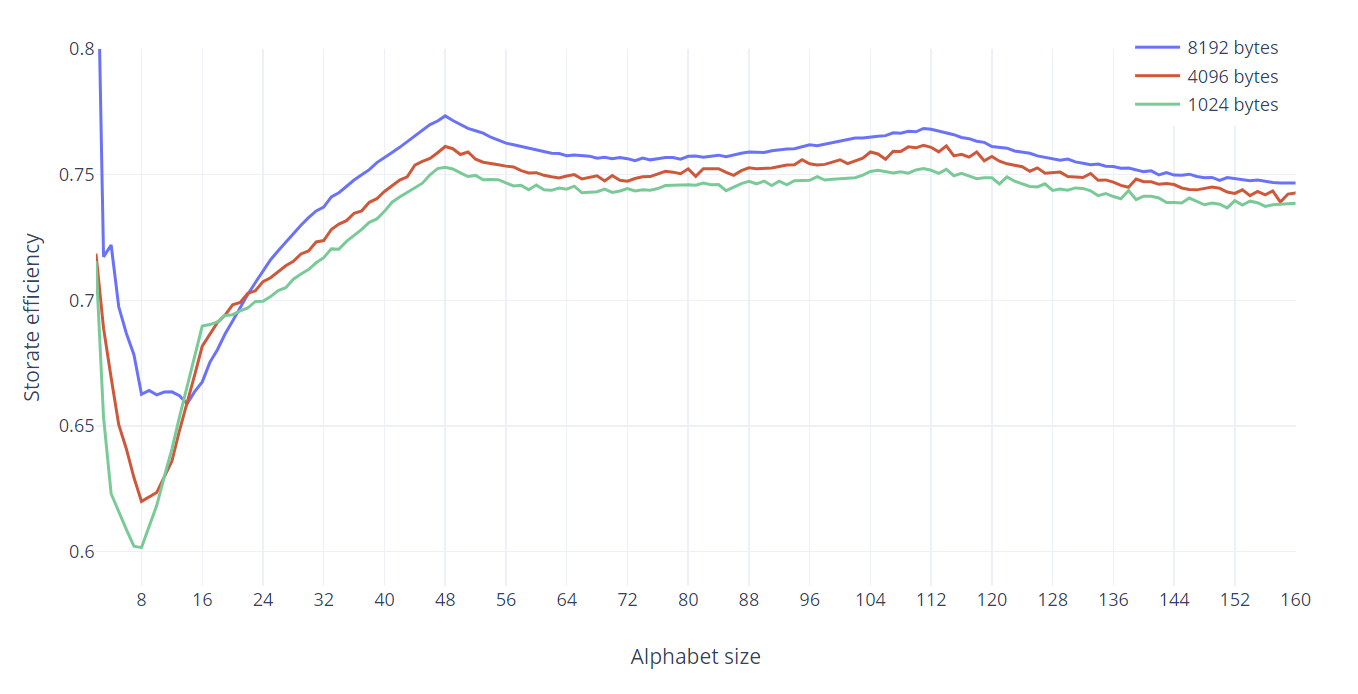
So, I had promised to revisit this after taking back references into account. Here are the experimental results for storing 1024, 4096, and 8192 bytes of information as a string in a PICO-8 cart (new format). The results do not change much, still the two peaks at N=48 and N=112, except for a surprising peak for N=2. This means that for large amounts of data, encoding as binary (x="01010000100…10010010011") is more efficient than any other format including hex or base64!

Whoa, wait, what? That's crazy, there must be some kind of compression optimization that's giving you close to an 8:1 reduction or something. Do back references really contribute that much optimization on their own?
Since 2-char alphabets inflate to much larger strings, I'm guessing you'd hit the uncompressed code limit before this extra data could be useful, but it's interesting nonetheless.

Is efficiency better towards the top of the graph or the bottom? It's not super clear what the number means. Is it just compressed size divided by uncompressed size?

@Felice it is compressed size divided by information size (i.e. before encoding). Higher is better. It can never be larger than 1 for random data, but if one wants to store data in the code section, the goal is to be as close to 1 as possible.
@shy no optimisation here, I’m afraid! It just means that the encoding method isn’t very efficient for random data, but that it’s slightly less bad for N=2. The main reason is that the compression format only allows back references of length 3 or greater, which become less and less common with larger alphabet sizes. But that choice makes the algorithm more efficient for average cartridges, so it’s a good trade-off.
@zep I have a suggestion for a non-breaking extension to the compression format; since the sequence "0 10 00000 xxxxx" can never happen (because back references of length ≤ 32 are encoded with the sequence "0 11 xxxxx"), use it as a header to encode up to 32 bytes of uncompressed data. Similarly, use "0 0 00000 xxxxxxxxxx" as a header for up to 1024 bytes of uncompressed data. The compressor may then use this as a fallback when things don’t go well. This is akin to the “stored” blocks in the DEFLATE format.

I'm still not clear on the ratio. You say it's "compressed size divided by information size", but also say it's better when it's close to 1, which would only happen if compression utterly failed and the compressed data was the same size as the information size.
I have to guess you meant to say it's more like "amount of bytes saved divided by amount of incoming bytes". Like, if you started with 100 bytes and ended up with 75 after compression, the ratio would be (100-75)/100 = 0.25. Is this correct?
Also, didn't zep completely change the compression method? It used to be a base64-optimized lzss-style encoder, but I understood the new one to be something that throws away past-data lookup in favor of a dynamic heuristic that constantly shuffles its concept of ideal octets so that it can refer to the most likely ones with very few bits. I'm not entirely sure your python script is really simulating the two compression types properly. I think it'd be more useful to actually generate carts with random data in them and average a set of compressed export sizes per alphabet size.

@Felice sorry, a few things were not clear it seems:
- we are in a case where compression utterly fails; the whole thread is about storing random data, which by definition cannot be compressed, so the ratio is always below 1
- also this is about the new compression algorithm (though the very first graph also shows how the old one behaved)
What I measure is how pathological the compression becomes depending on the alphabet size. What the numbers tell me is the following: if I have random (or hard to compress) data to store in the code section of my cart (for instance, a compressed image), and if my only concern is compressed code size, should I store it as base64, or hex, or binary, or something else?
I’ll try to explain the data another way:
-
The efficiency of 0.75 for an alphabet size of 64 means: if I have 1024 bytes of data, encode it into a base64 string (of length 1024/3*4 = 1366 characters) and store it in the code, it will use 1024/0.75 = 1366 bytes in the compressed code section of the cart.
- The efficiency of 0.75 for alphabet size = 240 means that if I encode these 1024 bytes of data to base240 (using all printable characters), I will get a 1036-character string, but it will still use 1024/0.75 = 1366 bytes in the cart.
About the new compression algorithm, it has two ways of encoding data, and is supposed to select the “best” one at each byte it tries to compress:
- the variable length encoding of bytes that you describe (though the “very few bits” you mention is still 6 bits, for the 16 most recently used bytes)
- a back reference lookup system, similar to old PICO-8 but slightly enhanced
There was no real need to test the VLE part of the algorithm because its efficiency can be computed exactly (that’s what the Python script does). With random data and a large enough alphabet size, the results are equivalent to the full PICO-8 0.2.0 behaviour.
To test the new compression algorithm in its entirety, I wrote my own compressor (the code is in on GitHub) and tested it on several GiB of test data (same as generating random carts for PICO-8 but much faster 😄). The second graph shows the efficiency of that compressor, which I believe to be equivalent to the PICO-8 one, because the data format is simple enough.

I dunno, Sam. I tested the actual cart compressor. I did multiple runs for randomized data with various alphabet sizes. My findings don't seem to match yours, or your projections. I find binary encoding to be just as bad as it ought to be.
I didn't test every alphabet size, just the obvious ones, but here are my results, and they look exactly like what you would expect, with the compression ratio of randomized data being pretty firmly in sync with the size of the alphabet the random data chooses from:
https://docs.google.com/spreadsheets/d/10XwtD0zRnUymY2F4I6u_qm3St5C7p74A9ZvDTOd_k3M/edit?usp=sharing
This is the cart I used to generate test carts to compress. Don't run it on the BBS. Look for the "how to use" comment towards the end and run it locally, following instructions.
Anyway, from what I can see, we should choose a solution that balances ease of decoding with compression ratios. Probably base128 would be best, since it's about 90% of what you get out of the best-case scenario and you don't have to do any weird base 222->256 base conversions, you just decode 8 bytes into 7 much the same way you do 4 bytes into 3 with base64.
For non-random data, I suspect hex or maybe base64 would be better, as they wouldn't obscure repeated information as much, but again, I think real-world testing would be better than conjecture or simulation.

@samhocevar: Ah, ok, I think I misunderstood what the graph was showing as well, but I've read through the latest comments and it makes sense now. I think you're right, the requirement for 3+ characters would make larger alphabets less likely to be take advantage of that. Then the low sizes must be demonstrating how effectively back references work to optimize unstructured data!
Like Felice mentioned, though, I do think that many images-encoded-as-strings probably have enough repetition for compression to kick in. This is really testing the limits of data that has no structure, so maybe the different results you are both getting is because even rnd() creates some structure in the strings it generates?

@Felice that’s not a very comprehensive test… you are omitting interesting values such as 48 or 112 (peaks in the character entropy efficiency graph), 85 (for Ascii85), or 41 (three base-41 digits can encode 16 bits with very little overhead).
Also, the cart uses the PICO-8 rnd() which is good enough for games but not for producing high entropy data, thus artificially increasing the efficiency results. For instance, 4938 characters of decimal data supposedly compress to 2778 bytes (135.64%). But there is no way PICO-8 can achieve that with truly random data; the actual value will be closer to 3050 (148.93%). Here is an example of more suitable content:
info"3453336311891412579975290311048771856127053634938007998737667420129126620771952619334241441888471739802192355425928120015991680362183390851167653445421255809209731793010157438742111317196790691704672226191550512824688310773817801864869720830513084687541368477621476263408852410829448715897729982355506939051420870695847011341593321453193609180783308641443589047375339078375985937805102116571673913783532584364126679900013988420645701669136850070062829494728260405010249342469532956834705159429869908899641565057648390473135642032418597381775689572909011940903683837548645888939220098962949689634502530983861473044654407156088591358246146839662499080903445381679970377889944663011018508416045139214125018633558129911322028332455809415279013325492222681338539906370894039674350055827713610680584690172015358129923060274692347780182364306739136866111795991143889482010406206779165848336494391991853484301562000630617556341667494671924097413418581873081819255874953192975684726022384190340482925992725118498102113603950022246229502417450707358758963045446724103522116338590373575602056174785892534078095283864589471313838344232333694277063935189678266823868042979390684122517491500716257325052521455510397631217996240079211195978563604975294730390988921899740627178431412158201525632604044202816220145667178292166832875103850850423222735208639999285011946634083959418472724995265009432471275502416649445279474071316096998846413219087405833690497265792068953049780493410939067928320479790166443768973869498193142850535601172733463880433885514098285511118314339572261012632139678377327465298807581631355607817781391193309942520828342321097618080829721006494494784247969623719438924945553029891081170347077577857668345620321531807480996184240025170536565888847962620235226205833392749251966023531625143121297036681384493748118072820899786197955151299584942447096215902111412162893881160816358825001000522834040200703761687393755016917411131127437055948841127808763102109929945024880854760699463044076844163513171687210625404311482821438106593694253666823951621837144954170025604427841683586439784205757397005659448828003899198170016954424191603299384222508956355902317671410963101366072259840193488911395473797312985918219485957920368692712503948163083948160751048245089590302459882164905977214465466113324988631388230701430270174628761452307716234416481979363624502458690840336666693416550870261296158405152169569744191742037573687577691601832614984681928384580727413351259817240908382062518102228063771491310247083825889019386962963743199537553913782911559895133577150746490102942079360944222537792947233888092856327992133301286141336983800090596591329461464032075310580917773405291515537174252582166105108173666042976439421440690643952183504351486823712964982709646498517767744721042726787892205500016834552601057524181119911677560567209187320006348155755480112599973069591732481706784896673184906377359367418373678050320584103592511082808427564501824191978287014782452761128063554482957780817771619256860882162827142653854505455593048525024291469617474201296771252160519465972226530293735661718900574116635553268725588403020635952207495669114205262457844026124452136604422743681529482589665782924777716268146091816051535068160691504934138020547910858912090364319780045823038414685549177005658855272321013715527891456001447029819733192331698973126464093944845439921242430249391112499102349460523627857899100699768783410044358912095712545332646428817591066493097484762197715101829729491854867642411373182962744434292904400220549454844227610161047232045290378852135226730707656396950745558521425024816971845140387573091827783480160354536820469862859039601301802359821301939418175734335153625873235479132940367195181568306987469067829997005579065732032077512172103928388938988107243215571825635331700868575250177038645837925204523673955844152817453198889175899799234348223545711018869034249769527800587534648963898406083777294305110203712531658896237695838068372131539978531471874853129397448725206377696188132808535831239282551775721875564283345885272797670461616493621933747048330659573067250379384153192213610544481671152248342690721997153838263656670258779456287115105987264516318695091859190463673445175014843614781851572928692720032848082407634903410134423093024365915440589662276703285668120911741118031445754699637209172505872920878594525715244598736010176518278327169733505868608028547672882142465183368638046157335603183610829717058525535685886570862166206551668329434380831821601836216611878706098440804722671287777417487451551188863556786969702377260491739333694586487615297224132800477126688916307495561824608548439546699915314758914806027563979738135341401171753274071603383554645406808153356964728439994982669581134624785161876295886856298478858079563729940970871716172548084547754570009442821743851955894663350387551774996847008345654457907513246182937697227684705456386474261569144164541191809106741618656657769453142969680" |
Finally, the results that involved no compression (stored data) are a bit meaningless in this context, because if the data is part of the code section, we also have code in that section and we certainly want it to be compressed. Adding some lorem ipsum Lua code to the test cart may force PICO-8 to compress the code and give you the numbers you need.
Here are the results, formatted like yours, from my compressor (it now compresses about 5% better than PICO-8 while still generating valid .p8.png files):
encoding | data | | | | compressed
#alphabet | size | chars | compressed | average | vs data
————————————————|——————|———————|—————————————————————|—————————|———————————
binary 2 | 2048 | 16384 | 3109 3096 3097 3112 | 3103.50 | 151.53%
quaternary 4 | 2048 | 8192 | 2962 2957 2951 2936 | 2951.50 | 144.11%
octal 8 | 2048 | 5462 | 3063 3069 3049 3058 | 3059.75 | 149.40%
decimal 10 | 2048 | 4933 | 3032 3044 3035 3057 | 3042.00 | 148.53%
hexadecimal 16 | 2048 | 4096 | 2885 2872 2867 2872 | 2874.00 | 140.33%
base41 41 | 2048 | 3059 | 2748 2757 2751 2726 | 2745.50 | 134.05%
base48 48 | 2048 | 2934 | 2692 2689 2697 2685 | 2690.75 | 131.38%
base64 64 | 2048 | 2731 | 2761 2717 2733 2729 | 2735.00 | 133.54%
ascii85 85 | 2048 | 2557 | 2744 2741 2743 2720 | 2737.00 | 133.64%
base112 112 | 2048 | 2407 | 2700 2692 2701 2713 | 2701.50 | 131.90%
base128 128 | 2048 | 2341 | 2721 2748 2730 2709 | 2727.00 | 133.15%
base222 224 | 2048 | 2099 | 2732 2734 2744 2738 | 2737.00 | 133.64%
raw bytes 256 | 2048 | 2048 | 2761 2740 2753 2777 | 2757.75 | 134.65%
|
That said, I fully agree with you that ease of decoding needs to be taken into account. In fact my next post will be about this! 🙂
@shy You are right, images encoded as strings are not good objects for this study. To keep that analogy, my focus here would be more like images compressed using ad-hoc code (such as px9), and then encoded as strings.

@Felice by the way, the fact that the code section may contain both easily compressible code and less compressible data (that PICO-8 would have decided to store rather than compress had it been alone in the section) is the rationale for the compression format extension I suggested to Zep. It would make all most of my experiments here useless, but it would be great 😄

I did say I didn't test every alphabet size. :) I was mostly concerned with looking into your claim that binary was better than other encodings for random data, which I was certain couldn't be right. In general, the smaller the alphabet, the worse the compression efficiency vs. original data size.
Oh, and I actually meant to comment on your "stored block" idea. I think that's a really good idea, since it's going to be common for advanced carts to contain both compressible and uncompressible data in contiguous chunks.
I hope @zep takes the suggestion, though maybe you should make it in its own Support/Bugs post since I think he's a lot more likely to pay close attention to one of those.
Also, if you care to, you could always share your implementation with him if you want that extra 5% you mentioned. Not sure what your policy on that kind of thing is. But I think he might not be able to use it, depending on speed, since I think he said it has to be fast enough to compress the cart on every keystroke for the status display.
[Please log in to post a comment]