i've discovered an issue with sqrt(), and it's not about overflow.
since pico-8 uses fixed-point, i don't expect sqrt() to be exact, but this behaviour is odd enough that it messes up some simple comparisons.
try the following:
> print(sqrt(3.75)) 1.977 > print(sqrt(3.8)) 1.9917 > print(sqrt(3.85)) 2.0063 > print(sqrt(3.9)) 2.0209 > print(sqrt(3.95)) 2.0355 > print(sqrt(4)) 2 > print(sqrt(4.05)) 2.0125 > print(sqrt(4.1)) 2.0249 |
you'd expect the results to keep increasing, but as you can see, right around 3.85, the result is greater than 2. at sqrt(4), it goes back to 2 as one would expect. it's a weird discontinuity and breaks some of my code.
the following program shows the discontinuity visually in a graph:
cls() for x=1,128 do y=sqrt(x/16) pset(x-1, 127-y*32, 7) end |
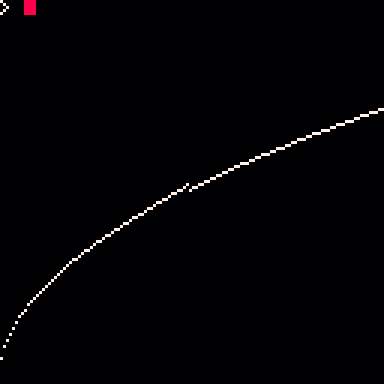
this is in pico-8 0.1.11g
thanks!

Confirmed on my Windows build:
> ?sqrt(3.85) 2.0063 > _ |
Not sure about other platforms.
Wonder if it's a lua-based sqrt() implementation and thus suffers from doing its work in fixed-point. That would be... a strange choice. I'd have expected sqrt() just to convert the result of the C lib version.
@zep?

Just noticed there's a discontinuity at 0.25 as well:
> ?sqrt(0.24) 0.4899 > ?sqrt(0.25) 0.5 > ?sqrt(0.26) 0.4987 > _ |
If anything, it's like the entire range of 0.25..2.0 is shifted up on the graph.

Just noticed there's a discontinuity at 0.25 as well:
> ?sqrt(0.24) 0.4899 > ?sqrt(0.25) 0.5 > ?sqrt(0.26) 0.4987 > _ |
Edit: Another at 9... maybe it's some kind of piecewise solution that's not calculating very well with fixed-point, so the endpoints of each section aren't matching up as they should.
Edit 2: Yeah, another at 16. Looks like it's in sections located between the squares of certain numbers, like 0.5, 1, 2, 3, 4, etc.

Sometimes I get too involved in very mundane subjects and spend way too much time writing code no one really wants.
The numbers are the left and right side x,y values, in hex.
Noteable (hex) values of X:
00.40 (1/4)
04.00
09.00
10.00 (16)
19.00 (25)
24.00 (36)

I discovered tonight that not only are there discontinuities, but at the two smallest values, the results are impossibly, code-breakingly wrong, not just in terms of precision or accuracy:
sqrt(0x0000.0002) == -0x0000.0004 |
You should never get a negative number from sqrt(). Inaccuracy will cause anomalies, but negative roots will break things.
This value should have been 0x0000.016A.
sqrt(0x0000.0001) == 0x0000.0000 |
0 can't be the square root of anything other than 0.
This value should have been 0x0000.0100, which is the exact square root of 0x0000.0001.
I've noticed that doing v^0.5 (which is another way to write √v in lua) produces exactly the same bugs as sqrt(v), so I'm assuming sqrt() simply returns v^0.5 and thus the bug is in the internal pow(b,e) function.
I'm sure you have all kinds of stuff torn apart and in progress, but is there any chance you could go to your archives, pull out the source for 0.1.11g, and do a hotfix for this? This keeps cropping up as a problem, at least for me. Usually it's just the discontinuitities, but tonight I chased a bug for an hour before I realized I couldn't assume sqrt() only returned positive numbers.

It gets worse. It's not just SQRT that's giving problems. The common solution for something like this would be to exponent a fraction.
cls() for x=1,128 do y=(x/16)^.5 pset(x-1, 127-y*32, 7) end |
This, too, does not work. :( So it's widespread, not just the SQRT command itself but the whole numbering system.
[Please log in to post a comment]