I'm porting this neural networks lib to pico8. But how I can see, int limit doesn't allow me to do that properly. The same code doesn't work on pico8:
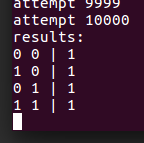
but works with lua 5.2:
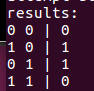
Is there a way to fix this?
Here is the full source code.

I guess you could try to implement your own version of a "big integer" (storing digits in an array). I did a crude implementation in my Picopolis game (https://www.lexaloffle.com/bbs/?tid=29590 look for "bint" functions), but it only supports adding and subtraction, and only positive values. If you need more functionality I'm sure there are articles on the internet on how to do that.

Check the exp() function. PICO-8 exponentiation works only with integer exponents. That is, PICO thinks 2^2 == 2^2.99.

Wait, do you mean, that I need another exp implementation, and that's it?

small chance, but exp (or the caret operator, not sure) is known to be borked, so that's the first thing to fix. there's a replacement here somewhere...

Replaced ^ with this: https://www.lexaloffle.com/bbs/?pid=30791#p30791
Seems to work ok:
exp(1) = 2.718 exp(0) = 1 exp(-1) = 0.3679 |

I wrote a similar implementation a while back. If there are any issues with that one, give this a try. They're both based on the same principles though so should give pretty much the same results.
function pow(v,e)
if(e<0) return 1/pow(v,-e)
local ei=band(e,0xffff)
local vi=v
e-=ei
local r=1
while ei!=0 do
if(band(ei,1)!=0) r*=vi
vi*=vi
ei=band(ei/2,0xffff)
end
while e!=0 do
v=sqrt(v)
if(band(e,0x.8)!=0) r*=v
e=band(e*2,0x.ffff)
end
return r
end
|
Edit: tried some numbers, including their examples. Mine seems to be slightly closer for negative powers. Dunno why, probably just rounds in the other direction due to operation ordering or something.

Not working correctly with both of them.
function pow(x,a)
if (a==0) return 1
if (a<0) x,a=1/x,-a
local ret,a0,xn=1,flr(a),x
a-=a0
while a0>=1 do
if (a0%2>=1) ret*=xn
xn,a0=xn*xn,shr(a0,1)
end
while a>0 do
while a<1 do x,a=sqrt(x),a+a end
ret,a=ret*x,a-1
end
return ret
end
function exp(x)
return pow(2.718,x)
end
|

Do you know the values x in exp(x) can range over during the run? If you're going over ~20.173 the results of exp(x) will wrap to negative.

If I read that right, the only place it calls exp() is in cell:activate(). My guess from the code that creates x, "-1*s/t", is that t is going to 0 somehow. This is because Pico-8 returns 32768 when you divide by 0. Basically, inf=32768. :)

Hm, that wouldn't do it. It'd have to be t. Or s could be 32768 from some other overflow and t might just be 1, I guess.
Maybe stick in a printh() that logs s,t at that point in cell:activate and see which one is causing the 32768 to get passed into exp.

Some output: https://pastebin.com/LNp6PJhd
So both t and s become 0 sometimes, that creates division by zero, that equals 32768.
It there a notification box on this forum? Will be really useful.

That was stupid... T==TRESHOLD, and TRESHOLD=0.
Anyway, there are still some problems with exp() argument overflow:
20.002 20.005 20.007 20.009 20.011 20.014 20.016 20.018 20.021 20.023 20.025 20.027 20.03 20.032 20.034 20.037 20.039 20.041 20.043 20.046 20.048 20.05 20.053 20.055 20.056 20.056 20.057 20.059 20.059 20.06 20.062 20.063 20.065 20.066 20.068 20.069 20.071 20.072 20.074 20.075 20.077 20.079 20.08 20.082 20.083 20.085 20.086 20.088 20.089 20.091 20.092 20.094 20.095 20.088 20.094 20.095 20.088 20.094 20.095 20.088 20.094 20.095 20.088 20.094 20.095 20.088 20.094 20.095 20.088 20.094 20.095 20.088 20.094 20.095 20.088 20.094 20.095 |
Updated code: https://pastebin.com/HXZS4c4S

Are those the maximum values for x in exp(x)? They're actually okay. We can handle up to 20.173. Looks like the code is currently set up not to overflow a signed 16-bit result.
...which is not to say that the very-large-but-legal result doesn't cause the next bit of math that uses it to overflow, I suppose.

If I train longer, x gets up and up, going more then up to 50.

Hmm. Is that value used for a specific purpose, or merely as a factor that allows cells to be compared relative to each other? I wonder if you could scale down x and get the same training results without overflowing.
Or use a smaller base, rather than 2.718. If you were to use, say, 1.1, you might get identical results while allowing an x up to 100 or so. Could be the person who designed the network only chose 2.718 because exp() was a convenient available function.
Lowering the base will reduce the precision of smaller x's though, as the least significant bits may get cut off of the 16-bit fraction. Looks like 1.1^x will bottom out for x=0.007 or so. So knowing the low end of x would be important too.

It's probably underflowing in the early stages, which is what I was worried about.
As I mentioned, the only other thing I can think of would be to try scaling x down by some constant fraction, maybe 0.125 or so. That would let you get up to 160 before it overflowed. I don't know how long you need to train before you get satisfactory results, though. Also, it might underflow early on too.
Otherwise... yeah, you might need a platform with proper floats, rather than fixed-point. To be fair to Pico-8, this is well outside of its comfort zone. :)

Yeah, but I just want to make it work :) Do you mean to scale it x*1.25 in exp or just try different values?

I was thinking something like this:
function exp_hacked(x) return pow(2.718,x*0.125) end |
I can't remember if that's basically the same thing as reducing the base, though. I can't remember the appropriate identities. At least it's easy to try. :)

I'm just looking at neurons signals, while the network is working. They just don't change at all, even after 10000 iterations.

Unfortunately, I know absolutely zero about neural networks, so beyond guessing at potential mathematical overflows, I can't think of anything else to suggest to work around it. If it needs very large and very small numbers, you might need either a software floating point implementation, or a string-based thing where you do the math longhand in ascii. Both would likely be slow, though I think software floats would probably do the best. It's no small endeavor either way.

Is there any reason you need to use a sigmoid activation instead of ReLu? ReLu's preferred for most applications anyway these days.... You'll have vastly reduced numerical issues and (probably) shorter training times. Unfortunately it looks like your code hard-codes knowledge of your activation function in the backprop step so you'll have to edit both forward and backward to get it to work. To be safe you might want to initialize your biases to some small positive value to make sure that all connections are live to begin with.
I can't guarantee this will help you, since I don't know for sure that the only bug is related to the exp in your activation. If not, you might try just implementing a network by hand: starting with functions for matrix multiplication and ReLu activation, then functions that implement forward/backward passes explicitly for your network, and finally the core training/eval loop. You can then verify the core functions you wrote along with the hard-coded network, and use its intermediate & final results to help debug the library.
For reference, see the first example from http://pytorch.org/tutorials/beginner/pytorch_with_examples.html (where it's just doing raw Numpy and before it gets into GPUs and autograd). Not sure why it uses random input/output; might be more interesting to use your xor dataset or some other meaningful function instead. Also note it omits biases.

Well, I'm an idiot. I just finished writing up a working xor example, which I didn't save while working on it ... and then typed
save(simplenn) |
to save it which crashed PICO-8 (https://www.lexaloffle.com/bbs/?tid=29585) and so now I have nothing to show you. But lessons learned would be:
- Use tables with size, stride, and data members to represent your matrices, and make sure to use strides in any operation that is not strictly element-wise. This will make creating and using transposed views easy and fast. Using tables-of-tables for matrices starts out nice but ends up nasty.
- You can learn xor with 1 hidden layer with 4 units and ReLu activation. Bad initialization can burn you with dead units, especially if you use the 0/1 formulation, but centering inputs and outputs (just replace 0 with -1) works basically every time.
- For bias you will need to broadcast and sum over rows (or columns -- with transposed views you just need to write one). I guess you could concatenate and slice instead, but that feels uglier to me.
- Learning rate of 0.01 is fine.
- If your network isn't learning, make sure that you're actually applying your activations and verify the correctness of your gradients at every step.
- Liberally use assert() to check the dimensional compatibility of matrix operation arguments. This will help catch bugs early.
[Please log in to post a comment]









