Simple Voronoi diagram generator. I was trying to see if I could get a speed boost from writing pixel values directly to the video RAM, but regardless the fill walking through all the pixels is still very slow. Any ideas on how I could speed things up?
--voronoi diagram
--by hypothete
points={}
function makepoints()
for i=1,16 do
e=rnd(128)
f=rnd(128)
add(points,{
x=e,
y=f,
c=rnd(255)
})
end
end
function jitter()
for i=1,#points do
p=points[i]
p.x+=rnd(2)-1
p.y+=rnd(2)-1
end
end
function near(pts,b)
nt=nil --nearest pt
nd=4096--dist to nt
for i=1,#pts do
a=pts[i]
nl=(b.x-a.x)^2 + (b.y-a.y)^2
--dist leaving off sqrt
if(nl<nd)then
nd=nl
nt=a
end
end
return nt
end
function drawvoro()
for i=0,63 do
for j=0,127 do
k=i+64*j --x+y*w = 1d position
z={x=i*2,y=j}
np=near(points,z)
if(np) then
memset(0x6000+k,np.c,0x1)
end
end
end
end
function _init()
makepoints()
drawvoro()
end
function _update()
if(btnp(5)) then
jitter()
drawvoro()
end
end
|

Not sure how much faster it'll make it, but I've heard using the ^ operator is slower than using a multiplication. So instead of (b.x - a.x) ^ 2 is slower than (b.x - a.x) * (b.x - a.x)

I can thing of a couple ideas.
The easiest seems to be fairly popular in Pico8 demos. Randomly choose which pixels to update each frame instead of using a for loop. The finished image will converge fairly quickly.
Another idea is algorithmic. You might want to google around, but I remember there being a algorithm that goes something like this: Find the closest two points and the difference of their distances. Advance that many pixels and then evaluate the closest two points again. You might be able to reduce the number of sorts using a hilbert curve or a recursive structure (that would be very rectfill friendly).

min2 version using circles and randomization also works pretty good. Converges quickly while minimizing edge artifacts.


Ok. I'm sort of having fun with this... Min2 version that skips along the x and interleaves scanlines:

A bit slower. Might try a recursive one that works by subdividing 8x8 blocks.
Here's an image showing pixels instead of drawing lines with lineskip.
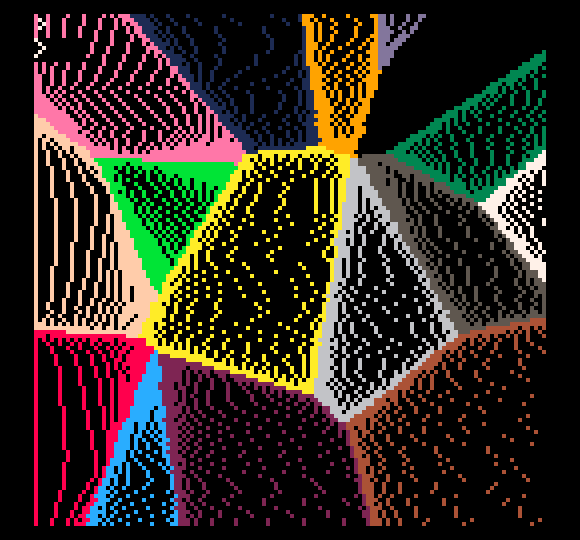

So the only really interesting thing in all of these is the modified near function:
function near2(pts, x, y) local p1, p2 = nil local d1, d2 = 0x7fff, 0x7fff for i = 1, #pts do local p0 = pts[i] local dx, dy = (x - p0.x)/16, (y - p0.y)/16 local d0 = dx*dx + dy*dy if d0 < d1 then p2, d2 = p1, d1 p1, d1 = p0, d0 elseif d0 < d2 then p2, d2 = p0, d0 end end return 8*(sqrt(d2) - sqrt(d1)), p1.c end |
It returns the nearest point, and the minimum distance you can go before it could possible swap with the next closest point.

Ok. Here's the code for all my experiments. Left and right change the algorithm, while up and down change the quality. The near2 monte carlo version is my favorite. It converges quickly, and is sort of a neat effect.
function jitter(points)
for i = 1, #points do
p = points[i]
p.x += rnd(2) - 1
p.y += rnd(2) - 1
end
end
function near(x, y, points)
local p1
local d1 = 0x7fff
for i = 1, #points do
local p0 = points[i]
local dx, dy = (x - p0.x)/16, (y - p0.y)/16
local d0 = dx*dx + dy*dy
if d0 < d1 then
p1, d1 = p0, d0
end
end
return p1.c
end
function near2(x, y, points)
local p1, p2
local d1, d2 = 0x7fff, 0x7fff
for i = 1, #points do
local p0 = points[i]
local dx, dy = (x - p0.x)/16, (y - p0.y)/16
local d0 = dx*dx + dy*dy
if d0 < d1 then
p2, d2 = p1, d1
p1, d1 = p0, d0
elseif d0 < d2 then
p2, d2 = p0, d0
end
end
return 8*(sqrt(d2) - sqrt(d1)), p1.c
end
function brute(points, res)
for y = 0, 128 do
for x = 0, 128 do
local c = near(x, y, points)
pset(x, y, c)
end
end
return "brute"
end
function vorocell(s, cx, cy, points, res)
local x0, y0 = s*cx, s*cy
if s <= res then
local c = near(x0 + 0.5, y0 + 0.5, points)
rectfill(x0, y0, x0 + s, y0 + s, c)
else
local s2 = s/2
local rl, c = near2(x0 + s2, y0 + s2, points)
if rl > s2*1.41 then
rectfill(x0, y0, x0 + s, y0 + s, c)
else
local cx2 = cx*2
local cy2 = cy*2
vorocell(s2, cx2 + 0, cy2 + 0, points, res)
vorocell(s2, cx2 + 1, cy2 + 0, points, res)
vorocell(s2, cx2 + 0, cy2 + 1, points, res)
vorocell(s2, cx2 + 1, cy2 + 1, points, res)
end
end
end
function subdivide(points, res)
vorocell(128, 0, 0, points, shl(1, res - 1))
return "subdivide"
end
function runlength(points, res, frame)
for y = frame%res, 128, res do
local x = 0
while x < 128 do
local rl, c = near2(x, y, points)
-- Clamp the run length to 1.
-- Rounding helps remove aliasing.
rl = max(1, flr(rl + 0.5))
line(x, y, x + rl, y, c)
x += rl
end
end
return "runlength"
end
function montecarlo(points, res)
for i = 0, res*50 do
local x, y = rnd(128), rnd(128)
local rl, c = near2(x, y, points)
circfill(x, y, rl, c)
end
return "montecarlo"
end
local points = {}
local res = 1
local frame = 0
local rendermethod = 1
local rendermethods = {
brute,
subdivide,
runlength,
montecarlo
}
function _init()
for i = 0, 15 do
add(points, {x = rnd(128), y = rnd(128), c = i})
end
end
function _update()
res -= (btnp(2) and 1 or 0)
res += (btnp(3) and 1 or 0)
res = max(res, 1)
rendermethod += (btnp(1) and 1 or 0)
rendermethod -= (btnp(0) and 1 or 0)
rendermethod %= #rendermethods
end
function _draw()
printh(rendermethod)
local render = rendermethods[rendermethod + 1]
local name = render(points, res, frame)
rectfill(0, 0, #name*4, 5, 0)
print(name, 0, 0, 7)
local fps = "fps: "..(30/stat(1))
rectfill(0, 6, #fps*4, 11, 0)
print(fps, 0, 6, 7)
frame += 1
jitter(points)
end
|

slembcke, these are remarkable, thanks for sharing! I'm going to try out line skip and your mixed shapes approach. Great idea on using monte carlo methods.

Ok. Last one I think. Near2 accelerated monte carlo with 32 regions and a jitter function that avoids clumping:

[Please log in to post a comment]