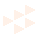Been working on a Tweetcart mimicking the old lines screensavers, and I've managed to get it pretty small--it's about 300 characters when all of the spaces are removed, but now I'm stuck, and can't figure out a way to shrink it any further.
Here's where I'm at so far:
a,b,c,d={},rnd,128,flr
for i=1,5 do
a[i]={x=b(c),y=b(c),w=b(c),h=b(c),p=d(b(4)),z=d(b(4)),l=i+7,m=mid,t=c}
end
::_::
for _=1,1000 do pset(b(c),b(c),0) end
for _𝘦𝘯𝘷 in all(a) do
d={[0]=1,-1,-1,1}
line(x,y,w,h,l)
x+=d[p]
y+=d[(p-1)%4]
w+=d[z]
h+=d[(z-1)%4]
p,z=x+y!=m(0,x,t)+m(0,y,t)and(p+1)%4or p,w+h!=m(0,w,t)+m(0,h,t)and(z+1)%4or z
end
flip()
goto _ |
This renders a result I'm happy with:
But it's just ~60 characters too long. :( Any one have any advice or suggestions on ways to reduce it further? I feel like there have to be some minimization techniques I'm missing.

I think you cut eight characters by changing your first for loop like this:
a,b,c={},rnd,128
for i=1,5 do
a[i]={x=b(c),y=b(c),w=b(c),h=b(c),p=b(4)\1,z=b(4)\1,l=i+7,m=mid,t=c}
end |
The cut is mostly not defining d as flr and using the \1 notation for integer division instead.
You may also not need the t=c assignment in your a table in the loop. Since it doesn't look like you're changing the value of t anywhere, you could just use c directly and that would cut another 4 characters.

beat me to it @2bitchuck!
@sizescape have you looked at using foreach instead of for in all()? I know usage would need to be quite different so I'm not sure if there's a net gain to be had there.
I'm sure that if it were shorter to define your own mid function with 0 and t (or c) hard-coded that you would have already done so.. but maybe there's a trick for that.
Same for using _draw, I don't suppose that's shorter than what you're using now.
You could save one character by opting for 999 black pixels per frame instead of 1000 ;)

Thanks @2bitchuck! Unfortunately, the t=c is needed, since overriding _ENV hides the global variables.
And @kozm0naut: Yeah, using functions makes things longer.
The current edge-collision detection code:
p,z=x+y!=m(0,x,t)+m(0,y,t)and(p+1)%4or p,w+h!=m(0,w,t)+m(0,h,t)and(z+1)%4or z |
is 77 characters, compared to
function g(a,b,c) return a+b!=m(0,a,t)+m(0,b,t)and(c+1)%4or c end p,z=g(x,y,p),g(w,h,z) |
Which comes in at 86. Similar problem comes up with foreach, since I'd have to define a function, which adds in the function, and end keywords--11 extra characters.
With your suggested changes, and changing the delta lookup-table to just be some bit manipulation, I was able to get a little further:
a,b,c={},rnd,128
for i=1,5 do
a[i]={x=b(c),y=b(c),w=b(c),h=b(c),p=b(4)\1,z=b(4)\1,l=i+7,m=mid,t=c}
end
::_::
for _=1,999 do pset(b(c),b(c),0) end
for _𝘦𝘯𝘷 in all(a) do
line(x,y,w,h,l)
x+=1-((p+1)&2)
y+=1-(p&2)
w+=1-((z+1)&2)
h+=1-(z&2)
p,z=x+y!=m(0,x,t)+m(0,y,t)and(p+1)%4or p,w+h!=m(0,w,t)+m(0,h,t)and(z+1)%4or z
end
flip()
goto _ |
Now it's just 41 characters too long to tweet after removing spaces.

I found something for you:
https://www.lexaloffle.com/bbs/?pid=49823
Seems we can drop the 0 argument from the mid calls altogether! Just a few tokens, but it's something.

2 bytes :
The ,0 of the pset statement could be omitted if the last line drawn had been black. This can be done by having l (the color parameter in lines) go from -5 to 0
for i=1,6 do
a[i]={x=b(c),y=b(c),w=b(c),h=b(c),p=b(4)\1,z=b(4)\1,l=i-6,m=mid,t=c}
end |
You may or may not prefer the old colours.
4 bytes from abusing the relative priorities of & and + :
x+=1-(p+1&2) y+=1-(p&2) w+=1-(z+1&2) h+=1-(z&2) |
This looks very wrong

@RealShadowCaster: Yeah, not a fan of the different colors. :(
Priority abuse inspired something else--I can use masks for doing the edge collision checks, instead of mid, if I make all of the positions integers, and I don't really need to constraint p and z to be in the range 0-3.
Brings it down to
a,b,c={},rnd,128
for i=1,5 do
a[i]={x=b(c)\1,y=b(c)\1,w=b(c)\1,h=b(c)\1,p=b(4)\1,z=b(4)\1,l=i+7,t=c}
end
::_::
for _=1,999 do pset(b(c),b(c),0) end
for _𝘦𝘯𝘷 in all(a) do
line(x,y,w,h,l)
x+=1-(p+1&2)
y+=1-(p&2)
w+=1-(z+1&2)
h+=1-(z&2)
p+=x&t|y&t>0 and 1or 0
z+=w&t|h&t>0 and 1or 0
end
flip()
goto _ |
Just 1 character to go (after spaces are removed)!
a={}b,c=rnd,128for i=1,5do a[i]={x=b(c)\1,y=b(c)\1,w=b(c)\1,h=b(c)\1,p=b(4)\1,z=b(4)\1,l=i+7,t=c}end::_::for _=1,999do pset(b(c),b(c),0)end for _𝘦𝘯𝘷 in all(a)do line(x,y,w,h,l)x+=1-(p+1&2)y+=1-(p&2)w+=1-(z+1&2)h+=1-(z&2)p+=x&t|y&t>0and 1or 0z+=w&t|h&t>0and 1or 0end flip()goto _ |

Nice trick with the binary 'or' operators, might have to use that elsewhere.
Used the tonum() boolean feature and got it down to 275 chars.
a={}b,c=rnd,128for i=8,12do
add(a,{x=b(c)\1,y=b(c)\1,w=b(c)\1,h=b(c)\1,p=b(4)\1,z=b(4)\1,l=i,t=c})end::_::for
_=1,999do pset(b(c),b(c),0)end
for _ENV in all(a)do
line(x,y,w,h,l)x+=1-(p+1&2)y+=1-(p&2)w+=1-(z+1&2)h+=1-(z&2)p+=tonum(x&t|y&t>0)z+=tonum(w&t|h&t>0)end
flip()goto _ |
And it actually seems to work basically the same without flooring the initial values (263 chars)
a={}b,c=rnd,128for i=8,12do
add(a,{x=b(c),y=b(c),w=b(c),h=b(c),p=b(4),z=b(4),l=i,t=c})end::_::for
_=1,999do pset(b(c),b(c),0)end
for _ENV in all(a)do
line(x,y,w,h,l)x+=1-(p+1&2)y+=1-(p&2)w+=1-(z+1&2)h+=1-(z&2)p+=tonum(x&t|y&t>0)z+=tonum(w&t|h&t>0)end
flip()goto _ |

Thanks everyone for your help! In case anyone reading the thread is interested in my thought process, here's a version of the cart with longer variable names, and comments describing what's happening:
lines={}
-- Initialize 5 colored lines at random positions
for i=1,5 do
lines[i]={
x1=rnd(128),
y1=rnd(128),
phase2=rnd(4),
x2=rnd(128),
y2=rnd(128),
phase1=rnd(4),
clr=i+7, -- colors 8-12 look nice
}
end
::start::
-- Draw 999 black dots, to fade out previous frames' lines.
for _=1,999 do
pset(rnd(128),rnd(128),0)
end
-- By assigning elements of lines to _𝘦𝘯𝘷, we don't need to use
-- dot notation to access the members of each table.
-- See www.lexaloffle.com/bbs/?tid=49047 for more details.
for _𝘦𝘯𝘷 in all(lines) do
-- Draw the line
line(x1,y1,x2,y2,clr)
-- Each of the endpoints of the lines should be incremented, with
-- the phase selecting how.
-- Phase[0], move left and down: ( 1, 1)
-- Phase[1], move right and down: (-1, 1)
-- Phase[2], move right and up : (-1,-1)
-- Phase[3], move left and up : ( 1,-1)
--
-- Note: Since the phase only increases, if an endpoint is moving
-- the 'wrong' way, it might need to make 3 left turns, instead of
-- 1 right turn to get back in bounds. When I showed the demo to a
-- few people, nobody noticed until I pointed it out, and even then
-- they didn't mind, so this is fine.
--
-- Easier to explain the following math for y:
-- if the phase is 0,1 want 1
-- if the phase is 2,3 want -1
--
-- Can compute this with:
-- 1 = 1-0
-- -1 = 1-2
--
-- If we generate a 2 when phase is 2 or 3, which we can
-- do by selecting bit 2 with "&2"
--
-- Since x's pattern is y's shifted by 1, just add 1 to phase, and
-- do the same computation.
x1+=1-(phase1+1&2)
y1+=1-(phase1&2)
x2+=1-(phase2+1&2)
y2+=1-(phase2&2)
-- Want to bounce if we hit the edge of the screen, i.e.:
--
-- if x less than zero or
-- x greater than 127 or
-- y less than zero or
-- y greater than 127 then
-- go to the next phase step
--
-- Since the 7th bit of the number will be set when it's first
-- negative or greater than 127, only need to check that to know
-- we should advance the phase, and 'turn'.
phase1+=tonum(x1&128|y1&128>0)
phase2+=tonum(x2&128|y2&128>0)
end
-- Slow down the animation to 30fps before looping.
flip()
goto start |
And the minimized (262 char) version:
a={}b,c=rnd,128for i=1,5do a[i]={x=b(c),y=b(c),w=b(c),h=b(c),p=b(4),z=b(4),l=i+7,t=c}end::_::for _=1,999do pset(b(c),b(c),0)end for _𝘦𝘯𝘷 in all(a)do line(x,y,w,h,l)x+=1-(p+1&2)y+=1-(p&2)w+=1-(z+1&2)h+=1-(z&2)p+=tonum(x&t|y&t>0)z+=tonum(w&t|h&t>0)end flip()goto _ |
Creates:

[Please log in to post a comment]