

I’ve been curious why smooth, textured curves were never a thing in graphics. Usually just polygons, or curves made out of polygons. After I saw this video on bezier curves, https://www.youtube.com/watch?v=aVwxzDHniEw thought I had enough tools to figure out why for myself. The video mentions two major difficulties when working with them: It’s hard to solve cubic polynomials, and estimating distance along a bezier curve isn’t precise.
If your goal is texturing them, it turns out you don’t even need to estimate distance. For any 2 bezier curves, they all share a start t value of 0 and an end t value of 1. You just have to scale up whatever t value you’re on to the height of your texture and draw your tline(), and it looks great!
The inability to solve cubic polynomials was tricky. Stack overflow has methods for drawing curves. I can’t quite figure them out, but they appear too slow for pico 8 and take a bit of space. Originally, I would just guess a T value and see if it was one pixel away, and go to the next one. Then I saw this video on newton's method https://www.youtube.com/watch?v=hHeq-SB8uVg
Which still uses guessing, but no checking and guessing again. And, if your first guess is close enough, you don’t even need to have a guess loop! I tried to put something together for that. Wowzers, you have to be really careful on how you approach +/- infinity. I had to precompute all the noteworthy points (the 2 local extrema, and the point in between) Newton's method acts up in areas of low velocity, so, I always approach the local extrema from t0, t1, or the time in between the extrema. (unless the point in between is starting to become a point of low velocity) When this cubic bezier function works, it’s such a nice smooth curve. I have it up on demo slide 2.
Picture generated in google using this equation: x-(393 x^3 +-552x^2+252x-39)/(3393x^2 + 2-552*x+252)
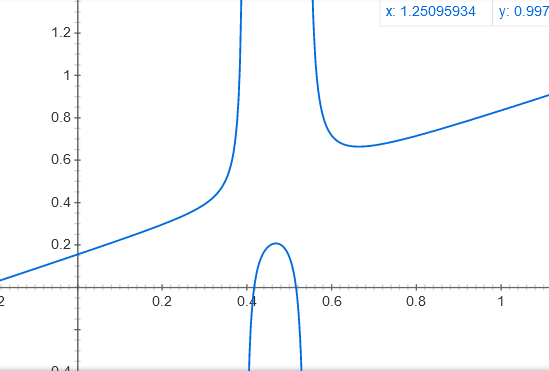
You can see when guesses start to go haywire. Newton's method is very delicate but very powerful for this sort of application
I also put together a quadratic(t^2) bezier function to compare with the cubic(t^3) one :
- A cubic function forming an “S” shaped curve is faster than 2 “C” shaped quadratics glued together making an S shape, but…
- There is now a whole lot of setup code for the cubic function, making it as long or longer than the solutions on stack overflow.
- The cubic bezier still uses a bit more of the cpu when zoomed out, but the quadratic scales down nicely. I think I would like to play games with several cool looping structures in the distance
- Glitches remain in the cubic one. Possibly solved by using quadratic bezier functions inside of it.
I think I will shelve the Cubic bezier for now. The Quadratic using Newton's method is nice, compact and fast, and is mostly functional.
The next step is to figure out how to rasterize it quickly. Which will be challenging with these angled tlines. Right now this demo runs at 30fps because I draw a tline at every pixel change. I hope it could be efficient enough to have a super fast racing game at 60 fps. But, I’m getting burnt out working on this. I think I’ll take a step away for a while.
The step after that is projection. From what I understand about 3d graphics, all one would have to do is project the 2 3d quadratic beziers (their 4 start and end points, and 2 control points), and one should, in theory, have a splendid textured curve in 3d space!
The demo on slide 1 uses some mode 7 type tricks to make it look like the texture is moving and going into the distance. If anyone wants to use a texture in a more standard way, I put in the function draw_textured_quad_bez() at the end (and quad_bezier_newton() above it) that accepts 6 screen control points and map tiles x,y + width/height in tiles. It mostly works pretty well! A sample is on demo slide 3.
TL;DR curved polygons?
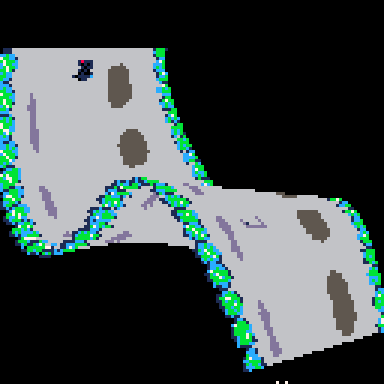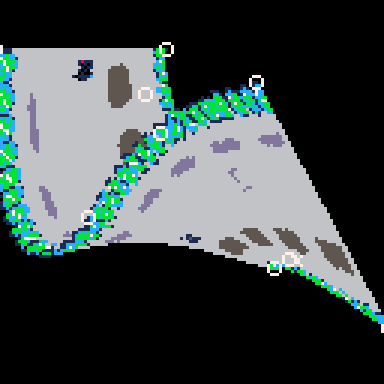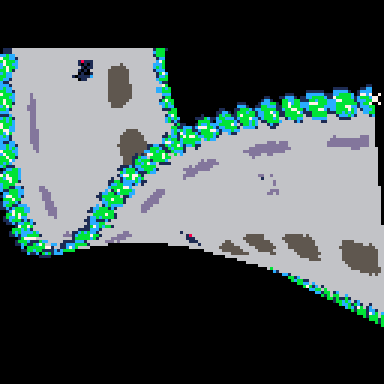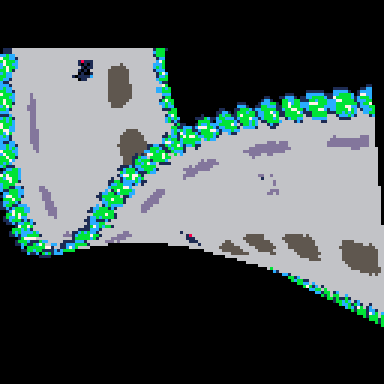

I think you have the potential of making a great racing game, like F-Zero for the N64 where the track goes all over the place, @ryzorm.
Here's a gold star to pave your way.

this is hella amazing, i want to render the Utah teapot with this, mind making a bezier triangle?

Yes! you're right @bloopa. There would be sharp edges on one axis if you modeled the utah teapot with these 4 sided Bezier curve polygons (it still might look really nice though). I don't think it's possible to make 3 sided ones? Maybe you could without using Beziers and instead use bell curves? But those use variable powers and may not be very efficient in Pico 8. Although, if you're not using textures, would it be possible using Beziers? hmm.
I'm still working on this slowly, on and off.
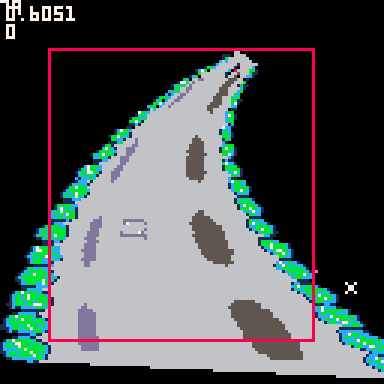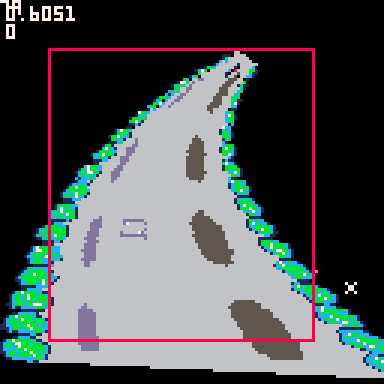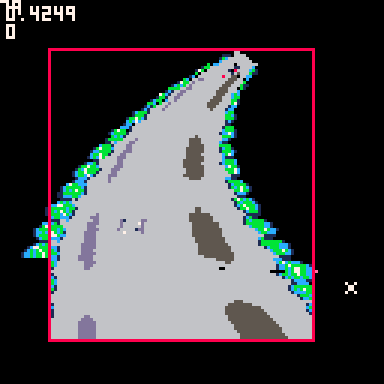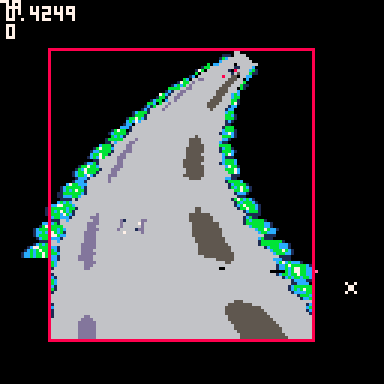
I got these curved polygons and regular polygons living side by side, kind of.

And I finally made progress making it efficient at rendering the track only on the screen, (which deals with degree 4 polynomials! and a little janky, but it's more efficient!)

@ryzorm bell curve formula looks like hell for performance because of its sqroot, im actually working on a software rasterizer and this could change how we render things in the future? i recommend finding a way to create bezier triangles, ill help too. also i recommend looking at zings algorithm for rasterizing Bezier curves :)
also i looked at the code, would this cause gaps on higher rez?

Thanks @dw817. Fixed. Worked fine a couple of months ago. I deleted some block comments. They must work differently now.
@bloopa I looked up zingls algorithm here https://zingl.github.io/Bresenham.pdf I abandoned that pretty fast because I needed the location of all pixels along the way to thread tlines between:

Those types of algorithms are more for drawing skinny lines. Using those algorithms would cause seams (gaps). I thought my solution was fast and small enough for Pico 8.
Thinking about doing curved triangles, so many problems come to mind. We will probably have to abandon the use of tline. We might have to solve an equation for every single pixel. The equation might involve powers or square roots.
These 4 sided ones are pretty cool, the Sega Saturn rendered only 4 sided polygons if I recall correctly. I would imagine an artist modeling and elephants trunk would have a pretty nice distinct look with these constraints.
But if you can help with 3 sides, maybe I could give it a shot. Does this BBS not have private messaging? You could probably find me somewhere online with my username. What kind of software renderer are you thinking of working on?
I'm pretty confidant this would not cause seams (gaps) at higher rez on modern machines. You only see seams in one of my demos cause I was trying some tricks to speed things up.
I implemented my idea on how to get depth working on my first post "The step after that is projection. From what I understand about 3d graphics, all one would have to do is project the 2 3d quadratic beziers (their 4 start and end points, and 2 control points), and one should, in theory, have a splendid textured curve in 3d space!"

@ryztorm https://blog.demofox.org/2019/12/07/bezier-triangles/
im just working on a software rasterizer based on https://www.youtube.com/watch?v=Y_vvC2G7vRo&list=PLEETnX-uPtBUbVOok816vTl1K9vV1GgH5 but in a data oriented language.
my discord is Matt_#1251 if you want to message there
also check out how tic80 textri demo does texture mapping https://tic80.com/play?cart=554

Wow! that first link has an actual webgl demo of a real life Bezier triangle that you can play around with! Never thought I'd see one! Thanks! I don't understand most of it, but it looks like it uses ray marching and hardware acceleration to accomplish what its doing.
Someone made a pico 8 raymarching demo. https://www.lexaloffle.com/bbs/?tid=51535 It's very slow, not feasible for a game. Possibly not feasible to use raymarching in a software renderer either? But maybe I don't know what I'm talking about.
[Please log in to post a comment]







