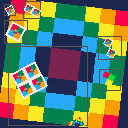
I was only able to find a few examples of rotating sprites using tlines on the forums. While the code worked, I couldn't really make sense of all the variables and magic numbers.
After spending quite a lot of time reading, debugging, and sketching hundreds of triangle, I think I have a decent understanding of the math and how it works. SOH-CAH-TOA haunts my dreams.
At some point, I'd like to make a more detailed post, but for now, I've written a tile rotating function with a lot of comments.
Hopefully it explains the math and the concept well enough that you can modify the code to suit your projects.
This code is intentionally not optimized or minified.
-- rtile -- draw rotated map tile -- x,y: output will be centered here -- tx,ty: map coords to the -- top,left tile to draw -- ang: rotation angle -- scale: scale factor -- default:1 -- tw,th: tiles to read -- default:1 -- tcxo,tcyo: -- tile center offsets -- in tile units -- default:0 -- nb: leave space around the -- tiles to rotate on the map -- or adjacent tiles may end -- up in the rotated output. function rtile(x,y,tx,ty,ang, scale,tw,th,tcxo,tcyo) local scale,tw,th= scale or 1,tw or 1,th or 1 local tcxo,tcyo= tcxo or 0,tcyo or 0 -- 8 is base tile->pixel scale scale*=8 -- precalculate a few values -- we need. using -sin because -- pico-8's sin func is inverted. local ca,sa=cos(ang),-sin(ang) -- there are two coordinate -- domains here, the input -- domain is in tile units -- and each tile has a domain -- of [0..1). the output domain -- is in pixels. we'll use "t" -- and "p" prefixes. -- what we're doing here -- is reading the source tile -- as a bunch of slices that -- stack up to form a square. -- we rotate that "reading" -- square and it changes how -- the input is read. the -- way we do this is with a -- rotation matrix that we -- apply to each point along -- one side of the "read" -- square. -- we need to know the center -- of the square for computing -- rotations. apply the center -- offsets here. -- tile center coords local tcx,tcy= tx+tcxo+tw/2,ty+tcyo+th/2 -- we're going to read the tile -- in a rotating square. if we -- use radius=tw/2, the corners -- will be clipped. we need the -- length from center to corner -- to use as the radius. we -- need to find the larger -- of the two radii to ensure -- the output fits. -- todo: make more efficient. -- tile radius local trad=max( sqrt((tx-tcx)^2+(ty-tcy)^2), sqrt((tx+tw-tcx)^2+(ty+th-tcy)^2)) -- to output the texture we -- draw a bunch of horizontal -- tlines. think of it as -- drawing scan lines on a -- display. using the p -- prefix to indicate "pixel". -- in order for the output to -- be the correct scale and -- not clip, we need to have -- a output space which can -- hold the rotated output. -- scale trad by 'scale' to -- get a pixel radius that -- will hold everything we -- need to draw. -- pixel radius local prad=scale*trad -- line scale is the ratio -- of read len/write len. -- this just makes a few -- calculations clearer. local lns=1/scale -- remember there are two domains. -- as we draw the output lines -- 0 to 2*prad, we increment -- from 0 to 2*trad proportionally. -- for every 1 pixel y in the -- output, we increment toffy -- by tstep. -- toffy range is -trad,trad local tstep,toffy=lns,-trad -- we also need to tell tline -- the step of the read lines. -- this controls how "far" -- each line reads in the tile -- domain. we want the length -- of the "read" line to be -- scaled to the length of an -- output line. local tdx,tdy=ca*lns,sa*lns -- now lets actually rotate the -- "read" lines. here's the formula. -- [cos, -sin][tx] -- [sin, cos][ty] -- because tx is not varied in -- the draw loop, we can pre- -- compute some values here. -- -trad is the "left" side -- of the read line. it's an -- x offset from the tile center. local costx=ca*-trad local sintx=sa*-trad -- visualize the output space. rect(x-prad,y-prad,x+prad,y+prad,5) -- we're going to draw a rect -- line by line, top down. -- because we're centering on -- x and y, add and subtract -- the pixel radius. for poffy=-prad,prad do -- now compute the ty values -- which is just the ty offset local costy=ca*(toffy) local sinty=sa*(toffy) tline( x-prad,y+poffy, x+prad,y+poffy, tcx+costx-sinty, tcy+sintx+costy, tdx,tdy) toffy+=tstep end end |
Here's the same code without comments if you just want to copy/paste in your project.
-- draw rotated map tile -- x,y: output will be centered here -- tx,ty: map coords to the -- top,left tile to draw -- ang: rotation angle -- scale: scale factor -- default:1 -- tw,th: tiles to read -- default:1 -- tcxo,tcyo: -- tile center offsets -- in tile units -- default:0 function rtile(x,y,tx,ty,ang, scale,tw,th,tcxo,tcyo) local scale,tw,th= scale or 1,tw or 1,th or 1 local tcxo,tcyo= tcxo or 0,tcyo or 0 scale*=8 local ca,sa=cos(ang),-sin(ang) local tcx,tcy= tx+tcxo+tw/2,ty+tcyo+th/2 local trad=max( sqrt((tx-tcx)^2+(ty-tcy)^2), sqrt((tx+tw-tcx)^2+(ty+th-tcy)^2)) local prad=scale*trad local lns=1/scale local tstep,toffy=lns,-trad local tdx,tdy=ca*lns,sa*lns local costx=ca*-trad local sintx=sa*-trad for poffy=-prad,prad do local costy=ca*(toffy) local sinty=sa*(toffy) tline( x-prad,y+poffy, x+prad,y+poffy, tcx+costx-sinty, tcy+sintx+costy, tdx,tdy) toffy+=tstep end end |
[Please log in to post a comment]