Here is a series of functions that are designed to be easily inserted into any project!
Each should be well commented and has a working example. comment if you have any questions!
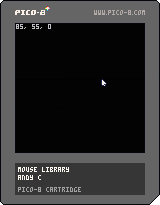
add a mouse function quickly!

move towards a target with a normalized speed (diagonals are not faster!)
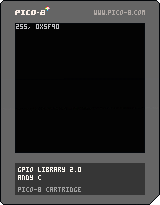
updated gpio library for (significantly) less tokens. now available for commercial use.
enter the pin (0 to 127) and return the hex (0x5f80 to 0x5fff) with get and set functions
old version included for posterity
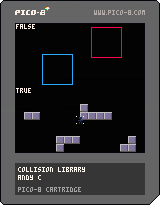
covers rect collisions and map flags; circ collisions are in lookatlib
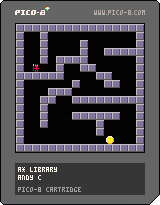
grid based path finding using A*
credit to https://www.lexaloffle.com/bbs/?tid=3131 and Pico8 Fanzine #4!

here are the examples:
With the exception of A*, the CC4-BY-NC-SA license only applies to examples and assets. The functions are all licensed CC4-BY. Please credit back to this blog post and not just my name so more people can use and learn from them.
The pathfinder function is a derivative of the example by richy486 https://www.lexaloffle.com/bbs/?uid=5758
please contact them if you wish to use the pathfinding function commercially.
--mouse library
--andy c
mouse = {
init = function()
poke(0x5f2d, 1) --activate devkit
end,
state = function()
return stat(32),stat(33),stat(34)
end,
curs = function()
spr(0,stat(32),stat(33))
end
}
function _init()
mouse.init()
c = {x=0,y=0,b=0}
end
function _update60()
c.x,c.y,c.b = mouse.state()
end
function _draw()
cls()
print(c.x..", "..c.y..", "..c.b)
mouse.curs()
end |
--gpio library 2.0
--andy c
function tohex(pin)
pin += 24448
return sub(tostr(pin,true),1,6)
end
gpio = {
--[[
the pins are the 128 values
between 0x5f80..0x5fff,
the pin values g0 from 0 to 127
value may be 0..255
to access the pins in
javascript:
var pico8_gpio = new array(128);
--]]
get = function(pin)
address = tohex(pin)
return peek(address),address
end,
set = function(pin,value)
address = tohex(pin)
poke(address,value)
end
}
--example of use
function _init()
gpio.set(16,255)
x,y = gpio.get(16)
end
function _update60()
end
function _draw()
cls()
print(x..", "..y)
end |
the GPIO library has been updated to save tokens and make the library safe for commercial use.
gpiolib1.0 is included in spoilers
--lookat library
--andy c
function atan(x1, y1, x2, y2)
--finds the angle between x & y
local x = x2 - x1
local y = y2 - y1
return atan2(x, y)
end
function distance(x1, y1, x2, y2)
return sqrt((x2 - x1) ^ 2 + (y2 - y1) ^ 2)
end
function lookat(x1,y1,x2,y2)
--steps x toward y
local x = cos(atan(x1,y1,x2,y2))
local y = sin(atan(x1,y1,x2,y2))
return x,y
end
--example
function _init()
obj = {x=63,y=63}
trgt = {x=rnd(127),y=rnd(127)}
end
function _update60()
vx,vy = lookat(obj.x,obj.y,trgt.x,trgt.y)
obj.x += vx
obj.y += vy
if abs(distance(obj.x,obj.y,trgt.x,trgt.y)) <= 1 then
run()
end
end
function _draw()
cls()
spr(1,obj.x,obj.y)
spr(2,trgt.x,trgt.y)
end |
controls: x or o - refresh; arrow keys - move little dude
--collision library
--andy c
function collision(r1x,r1y,r1w,r1h,r2x,r2y,r2w,r2h) --rectangular collisions
if ((r1x < r2x + r2w) and (r1x + r1w > r2x) and (r1y < r2y + r2h) and (r1y + r1h > r2y)) then
return true
else
return false
end
end
--[[
for circular collisions use: {where c is circle and r is radius}
if distance(c1x,c1y,c2x,c2y) <= 1/2 * (c1r + c2r) then
return true
end
distance can be found in my lookat library
--]]
function map_collision(r1x,r1y,r1w,r1h,flag)
check = false
for i=0,15,1 do
for j=0,15,1 do
if collision(r1x,r1y,r1w,r1h,i*8,j*8,8,8) and fget(mget(i,j),flag) then
check = true
end
end
end
return check
end
--example
function _init()
r1 = {x=rnd(97), y=rnd(33)}
r2 = {x=rnd(97), y=rnd(33)}
p = {x=0, y=72}
end
function _update60()
if btnp(❎) or btnp(🅾️) then
run()
end
if btn(➡️) then
if p.x < 120 then
p.x += 1
end
end
if btn(⬅️) then
if p.x > 0 then
p.x -= 1
end
end
if btn(⬇️) then
if p.y < 120 then
p.y += 1
end
end
if btn(⬆️) then
if p.y > 63 then
p.y -= 1
end
end
end
function _draw()
cls()
rect(r1.x,r1.y,r1.x+30,r1.y+30,8)
rect(r2.x,r2.y,r2.x+30,r2.y+30,12)
map(0,0,0,0,16,16)
spr(1,p.x,p.y)
print(collision(r1.x,r1.y,30,30,r2.x,r2.y,30,30),0,0,7)
print(map_collision(p.x,p.y,8,8,0),0,64)
end |
--a* library
--andy c
function pathfind(sx,sy,gx,gy) --thanks to picozine 4
showpath = false
showsearched = false
start = {sx,sy}
goal = {gx,gy}
frontier = {}
insert(frontier, start, 0)
came_from = {}
came_from[vectoindex(start)] = nil
cost_so_far = {}
cost_so_far[vectoindex(start)] = 0
while (#frontier > 0 and #frontier < 1000) do
current = popEnd(frontier)
if vectoindex(current) == vectoindex(goal) then
break
end
local neighbours = getNeighbours(current)
for next in all(neighbours) do
local nextIndex = vectoindex(next)
local new_cost = cost_so_far[vectoindex(current)] + 1 -- add extra costs here
if (cost_so_far[nextIndex] == nil) or (new_cost < cost_so_far[nextIndex]) then
cost_so_far[nextIndex] = new_cost
local priority = new_cost + heuristic(goal, next)
insert(frontier, next, priority)
came_from[nextIndex] = current
if (nextIndex != vectoindex(start)) and (nextIndex != vectoindex(goal)) then
if showsearched then
mset(next[1],next[2],19)
end
end
end
end
end
current = came_from[vectoindex(goal)]
path = {}
local cindex = vectoindex(current)
local sindex = vectoindex(start)
while cindex != sindex do
add(path, current)
current = came_from[cindex]
cindex = vectoindex(current)
end
reverse(path)
for point in all(path) do
if showpath then
mset(point[1],point[2],18)
end
end
reverse(path)
for point in all(path) do
targetx = point[1]
targety = point[2]
end
end
-- manhattan distance on a square grid
function heuristic(a, b)
return abs(a[1] - b[1]) + abs(a[2] - b[2])
end
-- find all existing neighbours of a position that are not walls
function getNeighbours(pos)
local neighbours={}
local x = pos[1]
local y = pos[2]
if x > 0 and (mget(x-1,y) and not fget(mget(x-1,y),0)) then
add(neighbours,{x-1,y})
end
if x < 15 and (mget(x+1,y) and not fget(mget(x+1,y),0)) then
add(neighbours,{x+1,y})
end
if y > 0 and (mget(x,y-1) and not fget(mget(x,y-1),0)) then
add(neighbours,{x,y-1})
end
if y < 15 and (mget(x,y+1) and not fget(mget(x,y+1),0)) then
add(neighbours,{x,y+1})
end
---[[ for making diagonals
if (x+y) % 2 == 0 then
reverse(neighbours)
end--]]
return neighbours
end
-- find the first location of a specific tile type
function getSpecialTile(tileid)
for x=0,15 do
for y=0,15 do
local tile = mget(x,y)
if tile == tileid then
return {x,y}
end
end
end
end
-- insert into start of table
function insert(t, val)
for i=(#t+1),2,-1 do
t[i] = t[i-1]
end
t[1] = val
end
-- insert into table and sort by priority
function insert(t, val, p)
if #t >= 1 then
add(t, {})
for i=(#t),2,-1 do
local next = t[i-1]
if p < next[2] then
t[i] = {val, p}
return
else
t[i] = next
end
end
t[1] = {val, p}
else
add(t, {val, p})
end
end
-- pop the last element off a table
function popEnd(t)
local top = t[#t]
del(t,t[#t])
return top[1]
end
function reverse(t)
for i=1,(#t/2) do
local temp = t[i]
local oppindex = #t-(i-1)
t[i] = t[oppindex]
t[oppindex] = temp
end
end
-- translate a 2d x,y coordinate to a 1d index and back again
function vectoindex(vec)
return maptoindex(vec[1],vec[2])
end
function maptoindex(x, y)
return ((x+1) * 16) + y
end
function indextomap(index)
local x = (index-1)/16
local y = index - (x*w)
return {x,y}
end
function atan(x1, y1, x2, y2)
--finds the angle between x & y
local x = x2 - x1
local y = y2 - y1
return atan2(x, y)
end
function distance(x1, y1, x2, y2)
return sqrt((x2 - x1) ^ 2 + (y2 - y1) ^ 2)
end
function lookat(x1,y1,x2,y2)
--steps x toward y
local x = cos(atan(x1,y1,x2,y2))
local y = sin(atan(x1,y1,x2,y2))
return x,y
end
--example
function _init()
box = {x=1,y=1}
coin = {x=rnd(13)+1,y=14}
target = {x=0,y=0}
step = 0
end
function _update60()
pathfind(flr(box.x),flr(box.y),flr(coin.x),flr(coin.y))
vx,vy = lookat(box.x,box.y,targetx,targety)
if step >= 1 then
box.x += vx
box.y += vy
step = 0
end
step += .05
if distance(flr(box.x),flr(box.y),flr(coin.x),flr(coin.y)) <= 1 then
run()
end
end
function _draw()
cls()
spr(17,box.x*8,box.y*8)
spr(16,coin.x*8,coin.y*8)
mapdraw(0,0,0,0,16,16)
end |

Yo, so you can make some token and efficiency improvements to the collision library:
--collision library
--andy c
function collision(r1x,r1y,r1w,r1h,r2x,r2y,r2w,r2h) --rectangular collisions
return r1x < r2x + r2w and
r1x + r1w > r2x and
r1y < r2y + r2h and
r1y + r1h > r2y
end |
For map collision, you can actually go much further:
function map_collision(r1x,r1y,r1w,r1h,flag)
for x = max(0,r1x\8), min(15,(r1x+r1w-0x0.0001)\8) do
for y = max(0,r1y\8), min(15,(r1y+r1h-0x0.0001)\8) do
if (fget(mget(x,y),flag)) return true
end
end
end |
You can calculate the map coordinates that a rectangle covers using integer division by 8 (the \ operator), which will save a very significant number of cycles in the long run, especially when dealing with many checks. We also don't even need the rectangle collision function this way.
Lua numeric for evaluates the expressions only once (unlike other languages), so we can inline this integer division with the clamping for extra token and cycle efficiency. The clamps here are based on the same 16x16 map size you targetted but could be easily adjusted to make them parameters.
We can also return true directly within the for loop, which will save cycles if a collision is detected. I've used Pico8's shorthand if form too to save 1 token. I've also omitted any explicit return false since it adds cycles and tokens; this version returns nil which is falsy anyway.
The last quirk is the -0x0.0001, which is a correction for sub-pixel-perfect collision: a rect with x=0,w=8 would evaluate as covering the map tiles from x=0 and x=1, when what we probably want is for it to only cover x=0. Thanks to the brilliant and amazing decision to use 16.16-bit fixed-point numbers, we can easily correct by subtracting 0x0.0001, the smallest possible value. This means that any x that is even a hair larger than x=0 will cover both map x=0 and x=1 correctly.
I actually wrote my platformer logic for Find Gold to be sub-pixel-perfect for both collision and rendering and I've been meaning to get around to cutting it out and making it available as a snippet, but I wanted to make it more complete as a platformer library. It's collision mechanism is also more advanced, as it does sweep tests to calculate how far an entity can move along the given direction, although they are not full vector sweep tests and treat the axes independently (I believe I did horizontal first in order to give the player leeway on landing jumps).

@Ender42, I am looking at your mouse program. It shouldn't be that complex I think ...
Without comments it's quite a bit smaller.
function _init() poke(0x5f2d,1) end function _update() cls() x,y=stat(32),stat(33) spr(1,x,y) end |
[Please log in to post a comment]